https://dx.doi.org/10.14482/inde.41.01.611.072
Validación de resultados a través de algoritmo Montecarlo en procedimiento de calibración de temperatura
Validation of results through Montecarlo algorithm in procedure temperature calibration
Andrés David Gil Miranda*
Walter Serna Serna**
Lina Marieth Zuleta Gilon***
Correspondencia: Andrés David Gil Miranda. Carrera 27 n°. 10-02. Teléfono: 3226628244
Origen de subvenciones: Walter Serna Serna hace parte del proyecto "Generación semiautomática de funciones de transferencia para la discriminación de tejidos anómalos en imágenes médicas cerebrales a partir de comparaciones inter-sujetos" (Código 6-20-2), financiado por la Convocatoria interna para la financiación de proyectos de investigación año 2019
Resumen
Los organismos evaluadores de la conformidad (oec) acreditados por iso/iec 17025 realizan la validación de resultados, con el fin de confirmar mediante la revisión de competencia técnica la provisión de evidencia objetiva, evaluando el cumplimiento de los requisitos normativos necesarios para una aplicación específica [1]. La Guía para la expresión de la incertidumbre en la medición (GUM) proporciona dos alternativas para evaluar y expresar la incertidumbre de medición. La primera es una metodología basada en un modelo lineal de propagación de incertidumbre, y la segunda es un procedimiento alterno de propagación por simulación de Montecarlo (MCM) [2]. Si bien la primera alternativa es la más utilizada por los OEC, debido a su simplicidad, en este trabajo se propone usar la segunda alternativa basada en MCM como método de validación de resultados. Para esto, se presenta una guía de implementación de los algoritmos descritos en el suplemento 1 de la GUM, en el procedimiento de calibración de equipos de medición de temperatura con base en la norma técnica Thermometers, contact, direct reading: Calibration (nt vvs 103). Los resultados obtenidos muestran una tolerancia numérica aceptable, comprobando la efectividad de la herramienta propuesta en el uso de la metodología GUM validada mediante los procedimientos descritos en el suplemento 1.
Palabras clave: estimación de incertidumbre, propagación de incertidumbre, simulación de Montecarlo, validación.
Abstract
Conformity assessment bodies (oec) accredited by ISO/IEC 17025 perform validation of results, in order to confirm by technical competence review the provision of objective evidence, assessing compliance with the necessary regulatory requirements for a specific application [1]. The Guide to the Expression of Uncertainty in Measurement (GUM) provides two alternatives for evaluating and expressing measurement uncertainty. The first is a methodology based on a linear model of propagation of uncertainty, and the second is an alternative method of propagation by Monte Carlo simulation (MCM) [2]. Although the first alternative is the most used by OEC due to its simplicity, in this work it is proposed to use the second alternative based on MCM as a method of validating results. For this purpose, an implementation guide for the algorithms described in Supplement 1 of the GUM is presented, in the calibration procedure for temperature measurement equipment based on the technical standard Thermometers, contact, direct reading: Calibration (nt vvs 103). The results obtained show an acceptable numerical tolerance, verifying the effectiveness of the proposed tool in the use of the GUM methodology validated through the procedures described in Supplement 1.
Keywords: Montecarlo simulation, uncertainty estimation, uncertainty propagation, validation.
Fecha de recepción: 19 de julio de 2022
Fecha de aceptación: 26 de noviembre de 2022
INTRODUCCIÓN
La metrología es la ciencia que asegura la calidad de una medición [3]. Diferentes actividades socioeconómicas y procesos industriales como la seguridad alimentaria, salud, análisis químicos, la industria farmacéutica, entre otras, dependen del resultado de una medición [4]. Con el fin de demostrar la confiabilidad y precisión de las mediciones, los procesos industriales son vigilados a través de los organismos evaluadores de la conformidad (oec), los cuales son trazables a los centros nacionales de acreditación [5]. Estos organismos evalúan los sistemas de gestión de los laboratorios mediante la norma técnica iso/iec 17025 versión 2017. Estos organismos están sujetos a procesos auditables con el fin de actuar con una capacidad técnica que les permita hacer seguimiento a los métodos de calibración usados en la validación de resultados estimados [6]. La guía para la expresión de la incertidumbre de medición (GUM) y la guía de propagación de distribuciones por un método de Montecarlo GUM suplemento 1 son presididos por el comité conjunto para las guías en metrología (jcgm) en sus numerales (100 y 101). Estos protocolos son estandarizados para la estimación de la incertidumbre de medición, siendo la segunda propuesta utilizada en menor proporción debido a la complejidad computacional del algoritmo de simulación [7]. La metodología propuesta por la GUM estima la incertidumbre; de medición con base en la ley de propagación de incertidumbres, esta consiste en caracterizar la cantidad de salida de una medición a una distribución gaussiana o una distribución t-Student escalada y desplazada [8]. Asumiendo un modelo lineal, la incertidumbre combinada es exactamente calculada dentro del marco de incertidumbre GUM [9].Sin embargo, debido a que los fenómenos asociados no siempre se consideran lineales, se debe calcular un factor de cobertura, el cual da origen a una incertidumbre expandida. Dicha situación se analiza en el anexo g de la GUM [10]. Según el teorema del límite central, es posible suponer una función de densidad de probabilidad (pdf) gaussiana para la cantidad de salida; a menos que haya una contribución dominante a la incertidum-bre combinada de una cantidad de entrada. En este caso, se debe asignar una distribución t-Student para la evaluación de solo un pequeño número de indicaciones repetidas [11]. Como alternativa a los modelos lineales, el suplemento 1 de GUM se basa en el concepto general de "propagación de función de densidad de probabilidad: pdf", conocida como método de simulación de Montecarlo (MCM); en el que la evaluación de la incertidumbre de la medición parte de la ecuación modelo del mensurando en función de los parámetros individuales de entrada o de influencia. Posteriormente, se determinan las fuentes significativas de incertidumbre asociando una pdf a cada una de estas. Finalmente, se generan muestras aleatorias que siguen dichas pdf, las cuales se evalúan en la ecuación modelo del mensurando, con el fin de conformar un nuevo conjunto de datos sobre los que será posible determinar su respectiva incertidumbre [7]. La iso iec 17025 presenta un requisito denominado el aseguramiento de validez de los resultados; proceso que debe ejecutar todo laboratorio de ensayo o medición, con el fin de someter los resultados estimados a técnicas estadísticas para la validación de incertidumbres y medidas de error. Es importante realizar un seguimiento planificado para asegurar la calidad del proceso de medición, por lo que la normatividad lo exige. Sin embargo, las técnicas utilizadas para hacer este aseguramiento son de carácter autónomo para cada laboratorio. De igual manera, este requisito sugiere [1]: realizar verificación de equipos sometidos a muestras certificadas de tipo materiales referentes; someter los equipos a instrumentos calibrados con una trazabilidad garantizada; realizar comprobaciones intermedias al equipamiento en ensayos rutinarios de medición; utilizar gráficos de control para evaluar el método de medición o el comportamiento de los patrones en dichas mediciones; entre otros.
Existen guías propuestas por los organismos internacionales que desarrollan la metrología. Sin embargo, no han estandarizado un proceso o protocolo para seguir. El Instituto Nacional de Normas y Medidas (nist) ha desarrollado un software de uso libre de manera online para la estimación de incertidumbre con base en la metodología MCM. Si bien este puede utilizarse como alternativa de validación de la metodología GUM, este desarrollo tecnológico no garantiza que el usuario tenga un conocimiento teórico y práctico sobre el algoritmo; lo cual pone en entredicho el concepto de la estimación de las fuentes de incertidumbres típicas asociadas a las metodologías de calibración. por esta razón, hace parte del mismo proceso de aseguramiento el estudio y la comprensión de los métodos de estimación de la incertidumbre. La evaluación de la incertidumbre, tal como la presenta la jcgm 100: 2008 o la iso/iec guide 98-1, se basa en la ley de propagación de las fuentes de incertidumbres de un sistema de medición. Sin embargo, la jcgm decidió iniciar una nueva revisión para profundizar la explicación de algunos aspectos para redefinir el concepto de intervalos de cobertura. Esto implica que no sea necesario la determinación de los grados efectivos de libertad, por lo que se puede prescindir de la fórmula de Welch-Sat-terthwaite en comparación con los métodos lineales [12]. Es importante mencionar que el algoritmo MCM no está sujeto a aproximaciones; además presenta un mejor desempeño cuando los modelos contienen términos no lineales o cuando existe una fuente de entrada no gaussiana que predomina sobre las demás. La metodología GUM utiliza la aplicación de métodos estadísticos clásicos (frecuencia) para la evaluación de fuentes de incertidumbre tipo a y b, lo que se considera como una combinación de incertidumbres inmersas en el método bayesiano de soluciones analíticas [13]. Existen trabajos previos que usan el método MCM para validar los resultados obtenidos por el método de la GUM en procesos de acreditación según iso/iec 17025 [16]. En algunos casos, la incertidumbre expandida estimada con el marco de la GUM y el método MCM no refleja diferencias significativas en la estimación de la incertidumbre. Esto se debe a que se realizaron en aplicaciones de modelos de medición lineales. Es allí donde la GUM se puede validar con MCM [14]. Por consiguiente, los métodos GUM y MCM estiman los intervalos de confianza de la incertidumbre de medida de forma similar. Debido a esto, toma mayor validez el criterio descrito por el suplemento 1 de la GUM, fundamentado en la propagación de la incertidumbre [15].
La propuesta presentada en este documento radica en la estimación de la incertidumbre de medición acatando las disposiciones descritas en el suplemento 1 de GUM, con el fin de validar la incertidumbre estimada desarrollada en el estándar GUM. Así, se establece un criterio de aceptación válido y se presenta una metodología alternativa para el programa de aseguramiento de la validez de los resultados, el cual es requerido en la norma técnica iso iec 17025 en su actual versión. El resto de este documento está organizado de la siguiente manera: en la sección 2 se exponen las metodologías de los enfoques utilizados para estimar la incertidumbre de medición. posteriormente, se detalla la experimentación de las metodologías desarrolladas. Seguido de esto, en la sección 3 se presentan los resultados obtenidos y, a partir de estos, en la sección 4 se concluye con base en la finalidad de este artículo. Por último, en la sección 5, se detalla la bibliografía investigada.
METODOLOGÍA
A continuación se analizarán las dos metodologías que pueden usarse para la estimación de la incertidumbre de medición; con una descripción precisa en cada etapa del proceso.
Determinación de la incertidumbre de medición enfoque GUM
El procedimiento de calibración de la temperatura (cadena de frío) utilizado en el laboratorio de metrología Audifarma S.A. se realiza con base en la norma técnica Thermometers, contact, direct reading: Calibration (nt vvs 103); la cual tiene un modelo matemático establecido en el que se relacionan las magnitudes de entrada , que se enuncian mediante esperanza matemática y su desviación típica. La esperanza matemática es considerada la mejor evaluación de cada variable aleatoria Xi denotada como xi. Dicha desviación generada se conoce como la incertidumbre típica u (x) asociada a x.
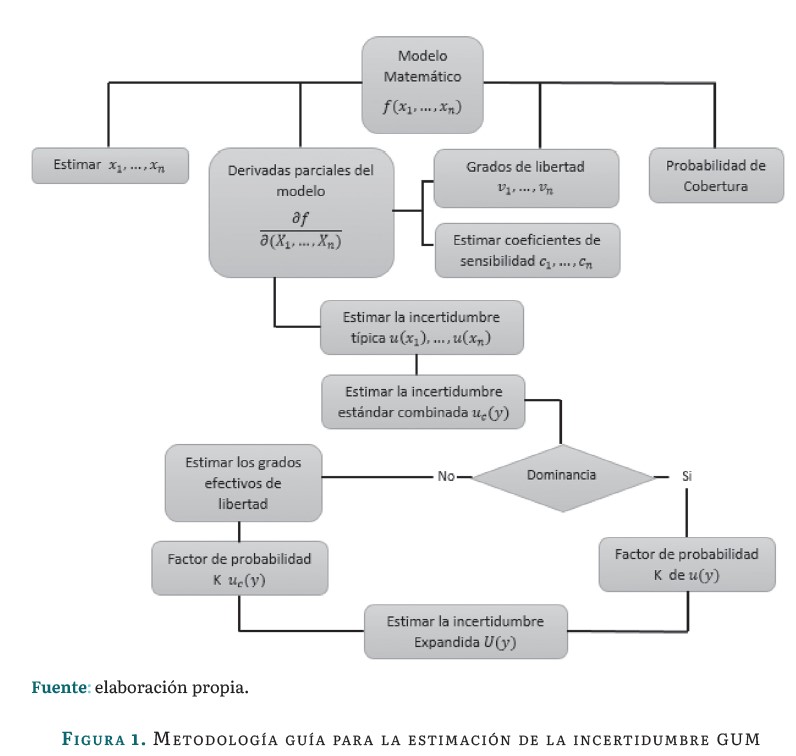
A continuación, se desarrolla la ley de propagación de incertidumbres, empleando la expansión de términos mediante las series de Taylor al modelo matemático establecido; lo que genera la estimación de la esperanza matemática de la magnitud de salida Y, la cual es una variable aleatoria de salida del modelo de medición, y a la que se le asocia una desviación conocida como la incertidumbre típica u(y) de y. Para brindar una mejor claridad, se invita al lector a realizar una breve consulta del numeral 5.6 del suplemento 1 de la GUM, el cual detalla la fundamentación teórica de las fases de propagación y resumen de evaluación para cálculo de la incertidumbre de medición [9]. En conclusión, la estimación yes el resultado del modelo evaluado de xi, de manera que se emplea un intervalo de cobertura para F cuyo fin es aproximar la función de densidad de probabilidad de salida como tipo gaussiana. En consecuencia, si el resultado de la estimación de los grados de libertad de u(y) tienden al infinito, se determina una distribución t escalada (Aplicación del teorema del límite central). En la figura 1 se exponen los pasos sugeridos de la guía para la estimación de la incertidumbre de medición GUM.
Determinación de la incertidumbre de medición por el método de Montecarlo
Esta metodología consiste en construir un modelo matemático del sistema de medición, en el que se asocian las variables que ingresan al sistema mediante un evento aleatorio o estocástico, el cual determina el comportamiento global del sistema de medición. Después de identificar las variables aleatorias, el algoritmo de Montecarlo propone, en primer lugar, generar muestras aleatorias para las variables de entrada al sistema y, en segundo lugar, analizar el comportamiento del sistema ante los valores generados.
El algoritmo MCM permite obtener una evaluación numérica g de la función de distribución gy(n). Seguido de esto, es posible representar las pdf de xi. De esta forma, es posible realizar una estimación de las propiedades de y, tales como los intervalos de cobertura, la varianza y la esperanza matemática, a partir de g. Entre mayor sea el número de muestras obtenidas de las pdf, se obtendrá una mejor estimación de los resultados. Sea yr, para r = 1,..., m, las muestras obtenidas la distribución de salida para el modelo y, las cuales permiten estimar la esperanza matemática e(Y), la varianza v(Y) y demás momentos estadísticos. Así, el conjunto de todas las muestras yr elabora una función de distribución que se asemeja a la función de distribución gy(n).
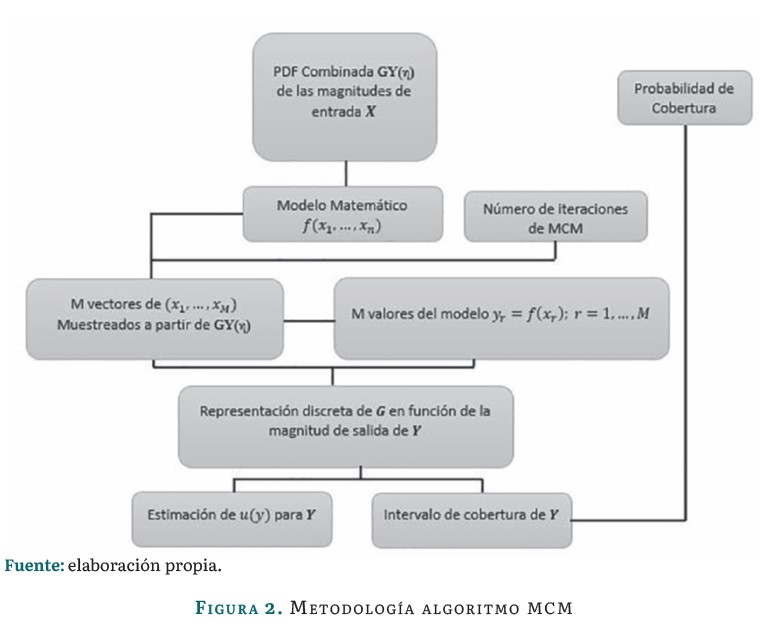
Luego, cada yr puede derivarse mediante un muestreo aleatorio de las pdf de x evaluadas en el modelo construido. Inicialmente, se obtiene la primera salida, la cual se conoce como g, y comprende los yr ordenados de manera ascendente. La virtud de MCM para establecer y, u(y) radica en el intervalo de cobertura de y, mientras se escoja un valor m adecuadamente mayor, la eficacia de esta metodología será mayor [9]. Este algoritmo se debe reiterar m veces, para así disponer de las m observaciones sobre el comportamiento del sistema. En la figura 2 se exponen los pasos sugeridos de la simulación del algoritmo MCM. Para más información, el lector se puede remitir al suplemento 1 de la GUM.
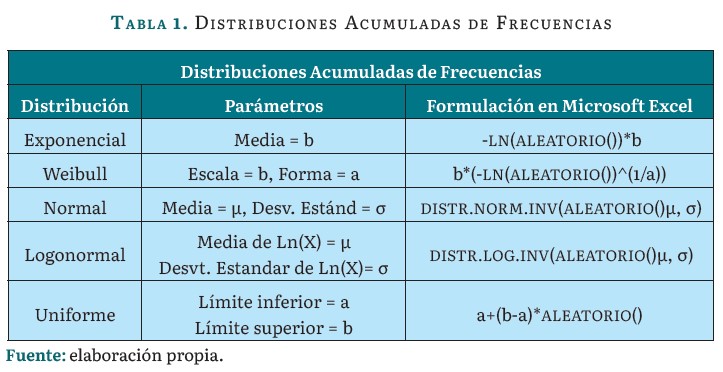
El algoritmo MCM se fundamenta en la generación de números aleatorios por el método de transformación inversa, el cual se aplica sobre las distribuciones acumuladas (ver tabla 1).
RESULTADOS Y DISCUSIÓN
Los datos de entrada para evaluar la estimación de la incertidumbre de medición mediante el enfoque GUM y el algoritmo MCM corresponden a las mediciones adquiridas de los dispositivos de medida que se utilizan en el laboratorio de metrología Audifarma s.a. los cuales son utilizados para realizar el aseguramiento de validez de los resultados. Estos datos provienen de calibraciones rutinarias y de propiedad confidencial del laboratorio de metrología.
Las mediciones realizadas estuvieron a cargo del equipo técnico del laboratorio, los cuales emplearon el procedimiento de calibración descrito en su sistema de gestión de referenciado bajo la norma técnica nt vvs 103:1994. Una vez ejecutado el algoritmo MCM, se realizó una etapa de validación para los resultados obtenidos. Este proceso consistió en comparar los resultados de la simulación MCM contra los resultados que emite el software desarrollado por el área de tecnología de la empresa Audifarma s.a. (datos de carácter privado). Adicionalmente, se contrastaron los resultados obtenidos en una hoja de cálculo desarrollada en el software Microsoft Excel, donde se detalla el paso a paso del proceso de estimación de incertidumbre, cuyo fin es obtener y comparar la incertidumbre de medición mediante la simulación del algoritmo MCM, utilizando el modelo matemático propuesto por la GUM. Los valores aleatorios generados en el software Microsoft Excel se obtuvieron mediante la función de distribución normal referenciada en la tabla 1. Los parámetros necesarios para dicha estimación provienen del cálculo tradicional de la metodología GUM.
Implementación enfoque GUM
Se realizó la comparación entre un termómetro digital de resistencia pt100 referente contra un equipo rutinario, a fin de obtener el estimado de la corrección en temperatura que se debe aplicar al equipo bajo calibración; dicha corrección está determinada por la ecuación 1. Las fuentes de incertidumbre típicas son las contribuciones que necesita el modelo matemático para desarrollar GUM. Las operaciones matemáticas realizadas son coherentes al expresar los resultados en la magnitud de temperatura, según el sistema internacional de unidades (si).

Donde

En la tabla 2 se relaciona el conjunto de operaciones para determinar cada incertidumbre típica que se asocia en la ecuación 1:
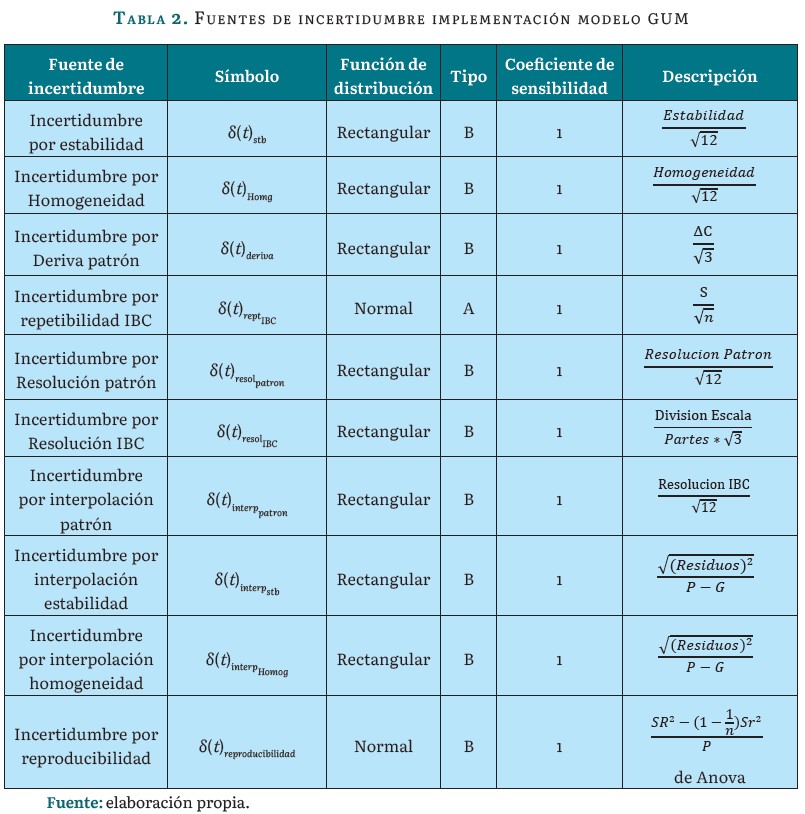
Una vez calculada cada fuente de incertidumbre típica de la tabla 2, se obtiene la incertidumbre combinada, el cual es el resultado al estimar la raíz cuadrada de la suma de las componentes (fuentes de incertidumbres típicas) de varianzas y/o covarianzas al cuadrado. Para estimar las varianzas y/o covarianzas se calculan los coeficientes de correlación o coeficientes de sensibilidad. La incertidumbre combinada se relaciona en la ecuación 2.
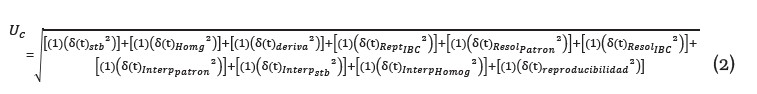
Estimada la incertidumbre combinada de la ecuación 2, se procede a estimar la incertidumbre expandida, la cual corrobora el criterio de proporcionar un resultado para la incertidumbre de medición dentro de un intervalo de probabilidad en el interior de una función de probabilidad tipo t-Student, esperando que dicha distribución cobije los valores del mesurando. Los grados efectivos de libertad, Veff, son calculados como lo establece la ecuación de Welch-Satterthwaite, la cual se relaciona en la ecuación 3. Dicha estimación produce el factor necesario para sobreestimar la incertidumbre combinada.
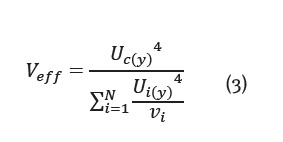
Donde

Finalmente, se estima el valor de la incertidumbre expandida con la ecuación 4:
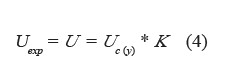
La GUM recomienda expresar el resultado de una medición de la forma y = y ± U. Esto se entiende como la mejor estimación para y. Así puede atribuirse el valor de Y a la corrección C en temperatura.
Implementación enfoque MCM
Se contempla cada fuente de incertidumbre típica exigida en el procedimiento de calibración, al igual que lo establece la metodología GUM (tabla 2), con la diferencia de que cada componente de incertidumbre típica se desarrolla como un evento aleatorio dentro de una fdp evaluada. A continuación, se presentará de manera detallada la formulación de evento aleatorio para cada fuente de incertidumbre típica (ver tablas 1 y 3). Cabe mencionar que la formulación se desarrolló en el software Microsoft Excel.
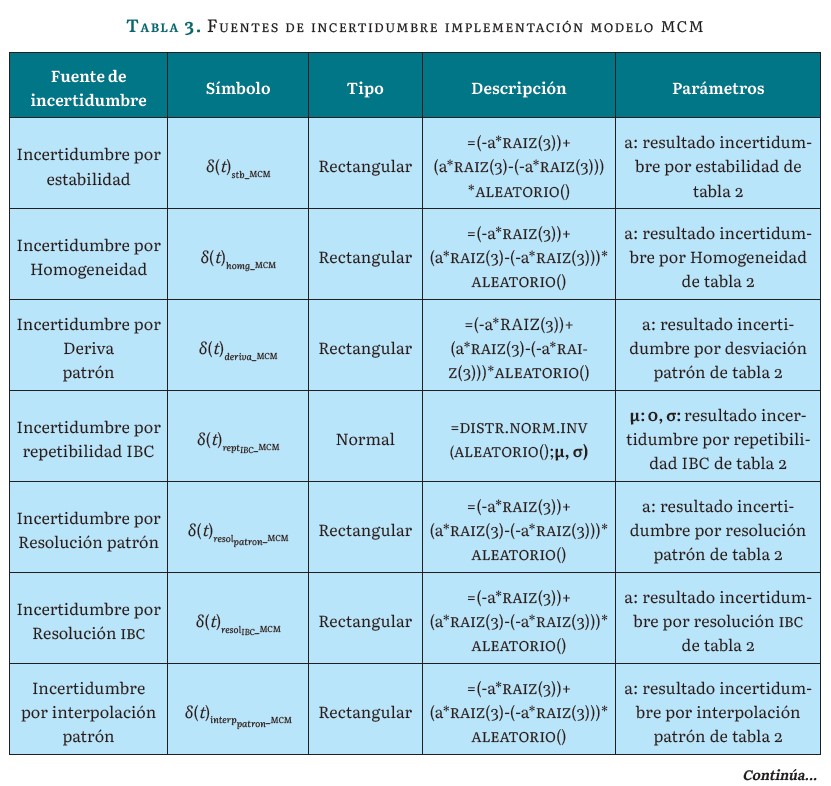
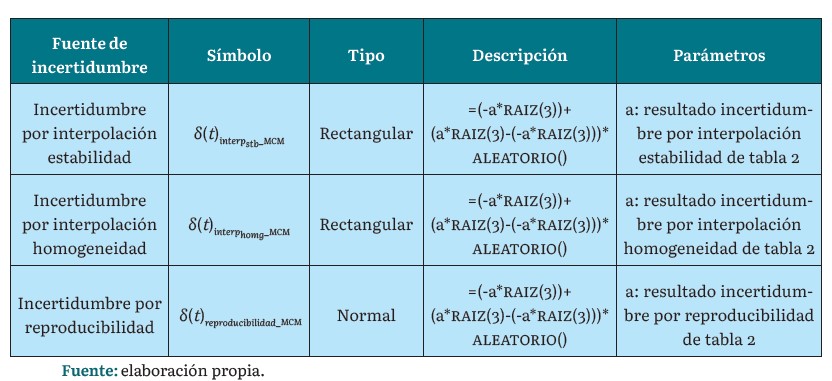
La implementación del algoritmo necesita un número de iteraciones establecido por el usuario para determinar el resultado al evaluar la ecuación 5. Una vez se ejecutan las simulaciones, se procede a calcular el promedio del conjunto de datos adquiridos, con el objetivo de establecer el valor medio de la distribución generada y así estimar la nueva función de densidad de probabilidad.
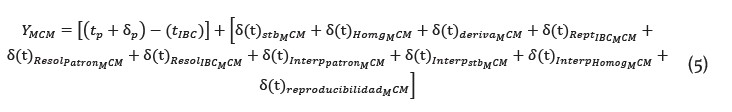
Por otro lado, se procedió a realizar el histograma de frecuencias para obtener una ilustración de la FDP. Finalmente, se formularon 2 metodologías para corroborar las estimaciones desarrolladas; en primer lugar, se ejecutó la propuesta de validación del suplemento 1 de la GUM. En segundo lugar, se evaluó el criterio de error normalizado.
Validación del enfoque GUM mediante el método de Montecarlo
Esta se realizó siguiendo la propuesta descrita en el numeral 8 del suplemento 1 de la GUM, el cual relaciona las ecuaciones 6, 7, 8 ,9 y 10 para desenvolver la siguiente propuesta:
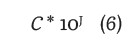
Donde C es considerado como el número de dígitos correspondiente a la incertidumbre estimada por la metodología GUM y / los decimales significativos de la misma.
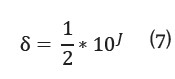
Por otro lado, se define S como la tolerancia numérica, la cual se utiliza para realizar el siguiente análisis. Estimar la diferencia entre las u (y) de cada metodología, comparando contra la tolerancia numérica S:
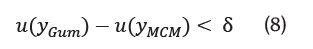
Si se cumple la inecuación, se valida GUM mediante la estimación de incertidumbre por la metodología Montecarlo. Para robustecer este análisis, se estiman las diferencias (inferior y superior) del intervalo estimado:
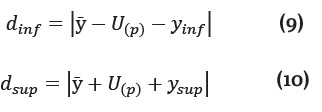
Dichas diferencias se relacionan con los límites de la función de densidad de probabilidad estimada. Así, si el límite inferior dinf y el límite superior dsup son menores que S, se valida la metodología GUM. Para más claridad ir a la referencia mencionada al inicio de esta sección.
Criterio de Error normalizado (En)
Con el fin de verificar si los valores son consistentes, según referencia bibliográfica [16], se cuantifica con la ecuación 11 la diferencia entre los promedios estimados a partir de cada metodología y la incertidumbre estimada. Se espera que esta diferencia esté por debajo de la incertidumbre del error.
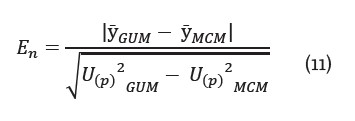
Donde

Protocolo de ejecución
Llamaremos algoritmo A al método empleado en el laboratorio de metrología Audifarma S.A. para estimar la incertidumbre de medición bajo la forma tradicional de la GUM (aproximación por serie de Taylor); de manera análoga, llamaremos algoritmo B a la metodología MCM. Se realizó la calibración por comparación de un termómetro digital de nevera marca Vici, modelo Tm803, con un patrón referencia fluke 1523 en la magnitud de temperatura (°C), la cual consiste en cálculo de la corrección en temperatura para un termómetro digital bajo la norma técnica Thermometers, contact, direct reading: Calibration (NT VVS 103). La ecuación para el cálculo de la corrección viene dada por la ecuación 1.
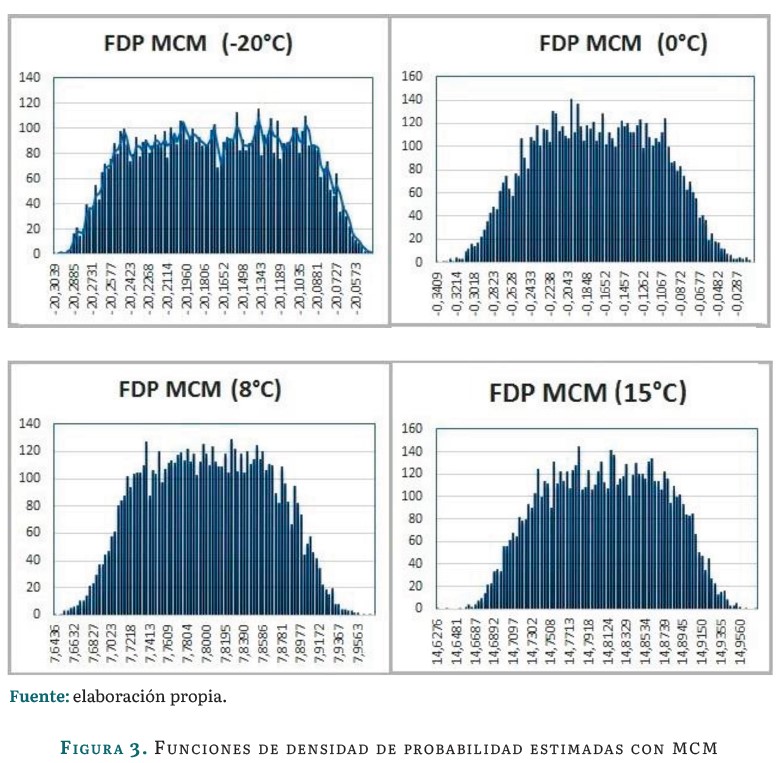
Se realizó la simulación del algoritmo B para conocer la convergencia en la estimación de la incertidumbre de medición con un número de iteraciones m=10, m=100, M=1000, M=10000 y M=100000 iteraciones (ver tabla 3). En la figura 3 se observan las funciones de densidad de probabilidad estimadas para las diferentes iteraciones realizadas en los valores referentes de la calibración.
De igual manera se utilizó la ecuación 11 para encontrar un segundo criterio de aceptación; estos resultados se pueden ver en la tabla 4.
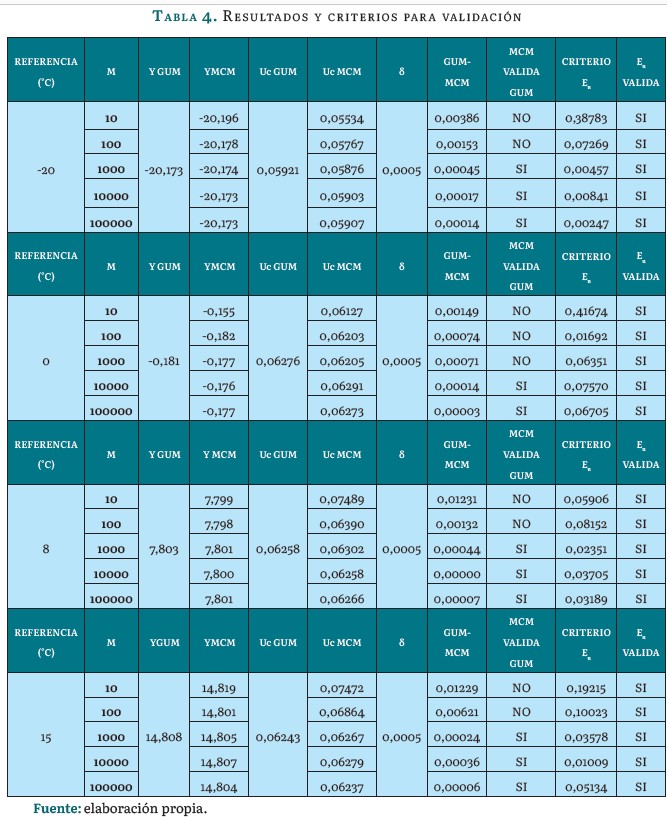
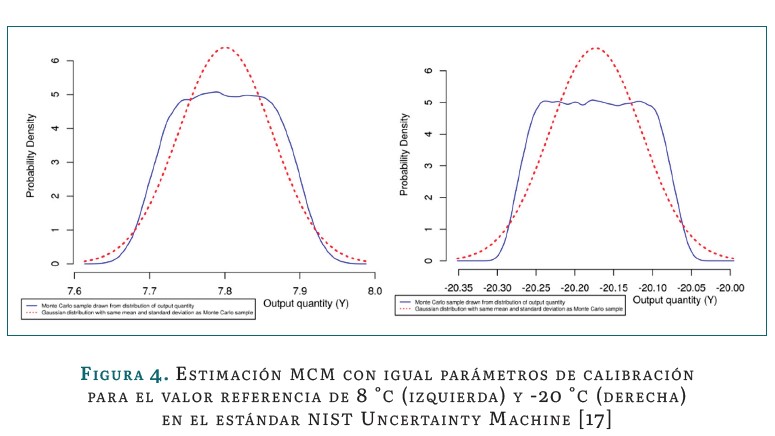
Para tener otro análisis objetivo, se realizó una comparación adicional de los resultados obtenidos contra el estándar de validación nist Uncertainty Machine, el cual es de licencia libre para uso rutinario y se encuentra en internet (enlace: https://uncertainty.nist.gov/). En este desarrollo se ingresaron los mismos parámetros de la ecuación (7) para el punto de calibración de -20 y 8 °c, seguido se sometió a una simulación para un m=100000. Los resultados se pueden ver en la figura 4.
DISCUSIÓN
Los resultados de la tabla 4, estimados bajo la metodología propuesta por el suplemento 1 MCM, necesitan un número m = 100000 repeticiones del algoritmo MCM para obtener un valor de estimación estable y confiable. Los resultados estimados, para un número de iteraciones por debajo de este valor, pueden arrojar una diferencia significativa según el criterio de la tolerancia numérica expresado en la ecuación 8; lo que indica que el método de calibración no sea reproducible. En los datos obtenidos de la simulación se tomó el valor promedio de la población de resultados como valor del mesurando, con el objetivo de expresar la incertidumbre combinada de la misma forma que se hace según el método GUM. Se observa que el valor estimado y el valor más probable coinciden en el caso en el que m = 100000 repeticiones, teniendo en cuenta que el suplemento 1 GUM sugiere este valor como mínimo para tener un intervalo de cobertura aceptable. Las funciones de densidad de probabilidad obtenidas en la figura 3 fueron desarrolladas para un m = 100 000repeticiones, las cuales son comparables y análogas con la figura 4 en los puntos de medición de -20°c y 8°c.
CONCLUSIONES
Tras el análisis realizado sobre las metodologías de estimación de incertidumbre de medición (GUM y MCM), podemos inferir que la metodología de simulación Montecarlo proporciona un protocolo definido de validación, que puede emplearse como un procedimiento para determinar y expresar de manera efectiva y eficaz el resultado estimado para la incertidumbre de la medición. A partir de la evidencia recolectada podemos demostrar que la prueba comparativa de error normalizado, cuyo fin fue obtener una medida de validación alternativa entre la metodología MCM para GUM, resulta ser satisfactoria para robustecer un procedimiento de validación dentro de un programa de aseguramiento de validez de los resultados.
De la tabla 4 podemos observar que las diferencias obtenidas en las incertidumbres combinadas expresadas bajo las metodologías GUM y MCM fueron en menor proporción con la tolerancia numérica expresada en la incertidumbre combinada de GUM. A medida que se aumentó el número M de simulaciones, se observó que esta diferencia se atenuó proporcionadamente, lo cual hace objetivo realizar el análisis para formular la validación y aceptación de la metodología GUM.
Se obtuvo dos incertidumbres combinadas de mediciones diferentes, desarrolladas bajo las dos metodologías propuestas, en la cual se realizó una prueba estadística de error normalizado expresada en la ecuación (6). Estos resultados se desarrollaron para los diferentes valores de M analizados. Estas pruebas fueron de carácter satisfactorio y se incluyeron en este informe con el fin de robustecer el análisis. Pese a ser satisfactorios en todos los casos de diferente número de iteraciones, se concluye que por ser diferencias tan poco significativas en los parámetros de incertidumbre, esta prueba sesga un resultado satisfactorio.
Pese a realizar la implementación del algoritmo MCM en una hoja de cálculo del software Microsoft Excel el cual presentó un adecuado desempeño, se comprueba que la simulación MCM se ejecuta mayor tiempo comparado con el software utilizado en el estándar de validación nist Uncertainty Machine, el cual está desarrollado en el lenguaje de programación r. Se puede concluir que la implementación en el software Microsoft Excel es de fácil uso, pero puede generar tiempos de espera prolongados en las simulaciones para un número M mayor de 100 000 repeticiones.
*Universidad Tecnológica de Pereira, Facultad de Ciencias Básicas. Pereira (Colombia).
Grupo de investigación Bioingeniería y Ciencias Forenses (bioif). Magíster en Instrumentación Física. andresgil@utp.edu.co.
Orcid id: https://orcid.org/0000-0002-2569-7209
**Universidad Tecnológica de Pereira, Facultad de Ingenierías. Pereira (Colombia).
Grupo de investigación Bioingeniería y ciencias Forenses (bioif).
Doctor en ingeniería (c). wserna@utp.edu.co. Orcid id: https://orcid.org/0000-0002-2965-1080
***Audifarma S.A. (Colombia). Coordinación del laboratorio de metrología Audifarma s.a. Química industrial. linazg@audifarma.com.co.
Orcid id: https://orcid.org/0000-0003-0499-8624
REFERENCIAS
[1] "Requisitos generales para la competencia de los laboratorios de ensayo y calibración", ISO/IEC, 2017.
[2] P. M. Harris y M. G. Cox, "On a Monte Carlo method for measurement uncertainty evaluation and its implementation", Metrologia, vol. 51, n°. 4, p. S176, 2014.
[I] J. Méndez Arias y L. Ramíez Varas, "Validación de la estimación de incertidumbre en la calibración de matraces para el método de sustitución simple sin masa de sensibilidad mediante el Método de Monte Carlo", Ingeniería, vol. 20, n°. 1-2, pp. 183-193, 2010.
[3] F. Khodabocus y K. Balgobin, «Implementation and practical benefits of ISO/IEC 17025: 2005 in a testing laboratory.,* University of Mauritius Research Journal, vol. 17, pp. 27-60, 2011.
[4] K. Gromczak, A. Gaska, K. Ostrowska, J. Siadek, W. Harmatys, P. Gaska y M. Kowalski, "Validation model for coordinate measuring methods based on the concept of statistical consistency control", Precision Engineering, vol. 45, pp. 414-422, 2016.
[5] D. Kurniadi y E. Amrina, "Designing ISO/IEC 17025: 2017-Based Laboratory Quality Manual: A Case of Laboratory of Environmental Engineering in Andalas University", International Journal ofProgressive Sciences and Technologies, vol. 19, n°. 1, pp. 14-21, 2020.
[6] G. Mahmoud y R. Hegazy, "Comparison of GUM and Monte Carlo methods for the uncertainty estimation in hardness measurements", International Journal of Metrology and Quality Engineering, vol. 8, p. 14, 2017.
[7] X.-l. Wen, Y. B. Zhao, D. X. Wang y J. Pan, "Adaptive Monte Carlo and GUM methods for the evaluation of measurement uncertainty of cylindricity error", Precision Engineering, vol. 37, n°. 4, pp. 856-864, 2013.
[8] K. Shimaoka, M. Kinoshita, K. Fujii y T. Tosaka,"Evaluation of measurement datasupplement 1 to the guide to expression of uncertainty in measurement-propagation of distributions using a monte carlo method", JCGM, p. 101, 2008.
[9] O. Seven y T. Supportedthe, "Guide to the Expression of Uncertainty in Measurement",
[10] M. G. Cox y B. R. Siebert, "The use of a Monte Carlo method for evaluating uncertainty and expanded uncertainty", Metrologia, vol. 43, n°. 4, p. S178, 2006.
[II] J. C. Damasceno y P. R. Couto, "Methods for Evaluation of Measurement Uncertainty", Metrology IntechOpen, pp. 9-28, 2018.
[12] Y. P. Paisan y J. P. Moret, "Determinación de la incertidumbre de medición por el método de Monte Carlo en los procesos de manufactura", Tecnología Química, vol. 28, n°. 3, pp. 56-62, 2008.
[13] M. A. Azpurua, C. Tremola y E. Paez, "Comparison of the GUM and Monte Carlo methods for the uncertainty estimation in electromagnetic compatibility testing", Progress In Electromagnetics Research, vol. 34, pp. 125-144, 2011.
[14] A. Jalid, "Comparison of the GUM and Monte Carlo methods on the flatness uncertainty estimation in coordinate measuring machine", International Journal of Metrology and Quality Engineering, vol. 7, n°. 3, p. 302, 2016.
[15] L. O. Becerra y L. M. Peña, "Evaluación del desempeño en los ensayos de aptitud de los laboratorios de calibración y el impacto en sus CMCs", Simposio de Metrología 2012.
[16] NIST, "Uncertainty Machine". [En línea]. Disponible en: https://uncertainty.nist.gov/. [Último acceso: 28 - 01 - 2022].