https://dx.doi.org/10.14482/inde.43.01.748.528
Efecto de la permeabilidad en el factor de seguridad de presas de tierra bajo precipitaciones
Effect of permeability on the factor of safety of earth dams under rainfall
Isaída Flores Berenguer*
Odalys Jacobo Rodríguez**
Samantha García Martínez***
Yoermes González Haramboure****
Jenny García Trístá*****
Correspondencia: Isaida Flores Berenguer. Teléfono móvil: (+53) 53100782. Dirección particular: Calle n.° 50 entre Avenida 25 y Avenida 27, Playa. La Habana, Cuba.
Resumen
En esta investigación se relacionan la permeabilidad y el contenido volumétrico de agua para evaluar su influencia en el factor de seguridad de presas de tierra homogéneas de 30 metros de altura. Para ello, se consideran cinco casos de análisis, incluyendo suelos arcillosos en el terraplén, uno para cada caso; un prisma de drenaje y una base impermeable. Estableciendo tres relaciones entre la permeabilidad y el contenido volumétrico de agua, a partir de los parámetros propios de los estudios de suelos y con el empleo de las ecuaciones de Terzaghi y Schlichter, se constituyen las condiciones fundamentales de la investigación. Se consideran cinco días de lluvia continua para tres intensidades, relacionadas con la permeabilidad saturada de cada suelo. Para ello, se emplea un modelo híbrido de elementos finitos y de equilibrio límite, mediante el programa GeoStudio (2018). El resultado permite establecer una relación entre el tiempo de falla, el método de estimación de la permeabilidad y el factor de seguridad para las intensidades de lluvia, observando que, con la aplicación del método de Schlichter, el factor de seguridad decrece abruptamente en las primeras 48 horas, mientras que para el método de Terzaghi, los resultados muestran una mayor similitud con los obtenidos a partir de los parámetros propios de los estudios de suelos.
Palabras clave: contenido volumétrico de agua, factor de seguridad, intensidad de lluvia, permeabilidad, presas de tierra.
Abstract
In this research, permeability and volumetric water content are related in order to evaluate their influence on the safety factor of 30-meter-high homogeneous earthen dams. For this, five analysis cases are considered, including clayey soils in the embankment, one for each case: a drainage prism and a waterproof base. Establishing three relationships between permeability and volumetric water content, based on the parameters of the soil studies and with the use of the Terzaghi and Schlichter equations, the fundamental conditions of the investigation are established. Five days of continuous rain are considered for three intensities, related to the saturated permeability of each soil. For this, a hybrid model of finite elements and limit equilibrium is used, through the GeoStudio (2018) program. The result allows establishing a relationship between failure time, the permeability estimation method, and the safety factor for the rain intensities, observing that, with the application of the Schlichter method, the safety factor decreases abruptly in the first 48 hours, while, for the Terzaghi method, the results show a greater similarity with those obtained from the parameters of the soil studies.
Keywords: earthen dams, permeability, rainfall intensity, safety factor, volumetric water content.
Fecha de recepción: 11 de septiembre de 2023
Fecha de aceptación: 11 de julio de 2024
INTRODUCCIÓN
La energía necesaria para que disminuya el contenido de agua en un suelo que presenta un grado de saturación inferior a la saturación total se conoce como "succión". La succión puede ser matricial, si se consideran los sólidos, u osmótica, si se consideran las sales disueltas. Además, representa la capacidad de un suelo parcialmente saturado a retener o no el agua contenida, generando para ello una tensión interna [1]. En un suelo parcialmente saturado, la conductividad hidráulica es variable y se relaciona de manera directa con la succión que se genera en el mismo [2], [3]. Para considerar la cantidad de agua retenida en el suelo parcialmente saturado debe tenerse en cuenta la porosidad del mismo y su grado de saturación inicial [4].
La variabilidad de las cargas hidráulicas a partir de la modificación de condiciones externas o de frontera a lo largo de un período de tiempo es la condición típica establecida en los análisis de flujo transitorio. Estados de filtración transitoria que generan condiciones de variación de la saturación y, por ende, modificación de las succiones, se pueden vincular a reducciones en los esfuerzos y los parámetros resistentes de los suelos parcialmente saturados, lo que puede conducir a la ocurrencia de deslizamientos de taludes [5], [6].
Estos deslizamientos ocurren cuando una parte del material, previamente estable, queda sujeta a un desplazamiento debido a una falta de apoyo a lo largo de una sección crítica, donde las fuerzas actuantes superan a las fuerzas resistentes del suelo. Un ejemplo claro de este fenómeno es apreciable durante los períodos lluviosos, asociados mayoritariamente a climas tropicales, en los que se generan flujos de agua transitorios vinculados a patrones de precipitaciones que modifican la infiltración en los suelos parcialmente saturados. La permeabilidad saturada total del suelo establece el posible intervalo de infiltración de la lluvia, y la intensidad y duración del evento controla el volumen de esta que podría infiltrarse [7].
Esta investigación plantea el estudio de dos elementos de un mismo problema: la relación entre la permeabilidad saturada y el contenido volumétrico de agua en los suelos parcialmente saturados y el efecto de la intensidad de lluvia, relacionada con la permeabilidad saturada del suelo, en la estabilidad de taludes. Para ello, se establece el análisis de una presa de tierra homogénea, estudiada para cinco casos diferentes, a partir de establecer cinco suelos como material de terraplén; los cuales cuentan con valores iniciales de permeabilidad y contenido volumétrico de agua obtenidos directamente. Luego se establecen nuevos valores de permeabilidad saturada, empleando las ecuaciones de Terzaghi y Schlichter, lo que permite plantear una relación entre la permeabilidad del suelo parcialmente saturado resultante. Con estos valores se fijan tres intensidades de lluvia para cinco días de duración, a partir de los cuales se obtiene el comportamiento del factor de seguridad del talud aguas abajo de la presa objeto de estudio. Estos resultados permiten relacionar el comportamiento del factor de seguridad con los valores de permeabilidad de los suelos arcillosos, así como predecir el tiempo en el que puede producirse la falla para diversas condiciones de lluvias establecidas.
METODOLOGÍA
Suelos parcialmente saturados
El análisis de las succiones en el laboratorio puede realizarse mediante diversos métodos, que se dividen en directos e indirectos, en dependencia del equipo que se emplee, así como el intervalo de medida de las succiones y el contenido de humedad presente [8]. Sin embargo, el empleo de estos métodos requiere equipo especializado y los ensayos resultan costosos y demorados. Por todo ello, han surgido modelos matemáticos de estimación de la curva característica, que son una alternativa viable cuando no se cuenta con datos experimentales que relacionen la succión con el contenido de agua. Existen diversos modelos que han demostrado una elevada precisión (superior al 75 %) respecto a la curva característica experimental de distintos materiales, como los propuestos por [9]-[11].
El método de [10] predice la función de contenido volumétrico de agua utilizando las propiedades básicas del material que pueden ser útiles particularmente para el análisis a nivel de anteproyecto. La función se determina inicialmente como una función de grado de saturación y luego se asocia al contenido volumétrico de agua (ecuación 1).






Relación entre la permeabilidad y el contenido volumétrico de agua en suelos
A partir de un estudio de los diversos métodos que existen para estimar la permeabilidad de los suelos se seleccionaron aquellos en los que se vinculaba este parámetro con el contenido volumétrico de agua, a partir de la porosidad.
Método de Terzaghi
Terzaghi introduce en su fórmula para el cálculo del coeficiente de permeabilidad (en cm/s) una constante que tiene en cuenta la porosidad y el tipo de suelo, como se muestra en las ecuaciones 5 y 6 [14].


Método de Schlichter
Este método introduce a la fórmula de Allen Hazen [14] una corrección por compacidad, en función de la porosidad, como se muestra en la ecuación 7, para obtener la permeabilidad (en cm/s) [14]


Análisis de estabilidad de taludes sometidos a precipitaciones
Los deslizamientos inducidos por la lluvia en suelos parcialmente saturados constituyen uno de los peligros naturales más recurrentes y destructivos en todo el mundo. La pérdida rápida de la succión matricial debido a la infiltración de la lluvia y el posterior desarrollo de presiones intersticiales positivas debido a la formación de un nivel freático elevado son los factores desencadenantes más importantes para esos deslizamientos.
La descripción matemática de este fenómeno se construye a partir de considerar los análisis de flujo de agua transitorios mencionado previamente. Para la obtención del factor de seguridad (FS) se propone en este estudio el método planteado en [15], que satisface las condiciones de equilibrio de fuerzas y de momentos, y presenta una elevada flexibilidad geométrica e hidráulica.
BASES PARA LA MODELACIÓN NUMÉRICA
En la figura 1 se presenta la geometría de la presa homogénea objeto de estudio.
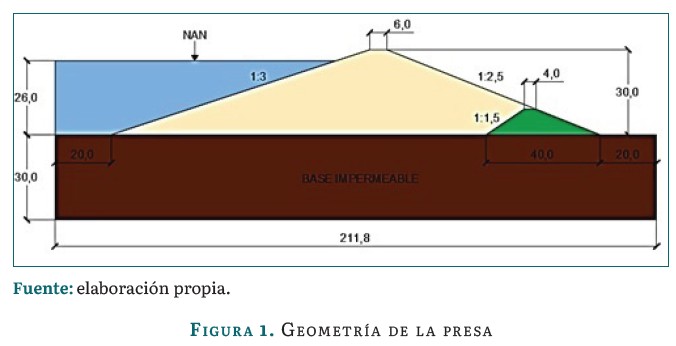
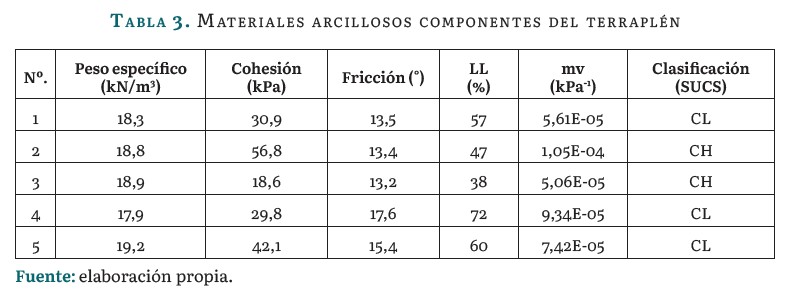
Las propiedades físico-mecánicas fundamentales de los cinco suelos empleados como material de terraplén, así como su clasificación (arcillas de alta o baja compresibilidad) mediante el Sistema Unificado de Clasificación de Suelos, se muestran en la tabla 3.
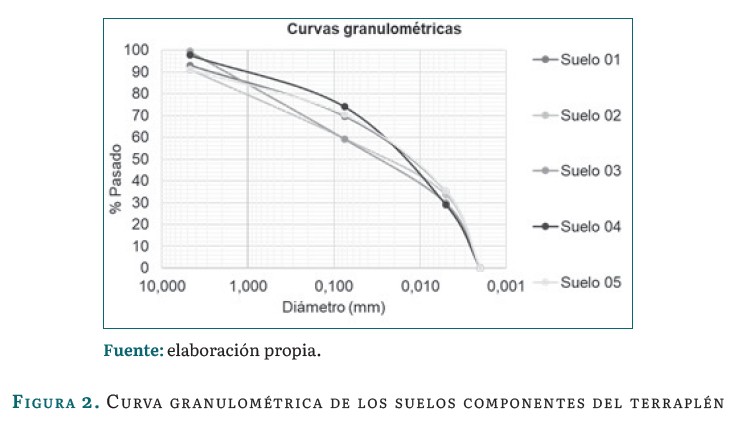
La figura 2 representa la curva granulométrica para los cinco suelos del caso de estudio.
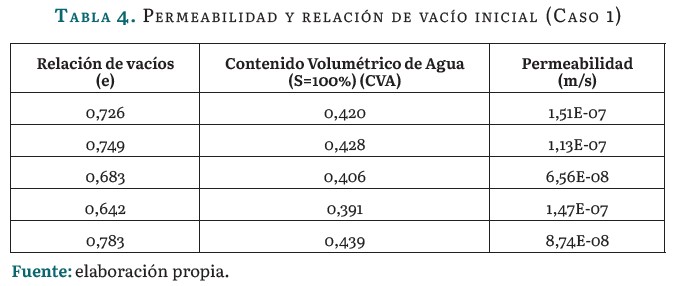
Para el análisis de la permeabilidad y el contenido volumétrico de agua (CVA) se establecen tres casos de estudio.
Caso 1: Permeabilidad y relación de vacío inicial correspondiente a cada suelo, como se muestra en la tabla 4.
Para este caso, se obtuvo el contenido volumétrico de agua a partir de la relación de vacíos del suelo, considerando una saturación de 100 %. La permeabilidad corresponde a los datos originales de los suelos estudiados obtenidas para los mismos en cada caso.
En la figura 3 se muestran las curvas de conductividad hidráulica correspondientes a los valores de permeabilidad y CVA de la tabla 4.
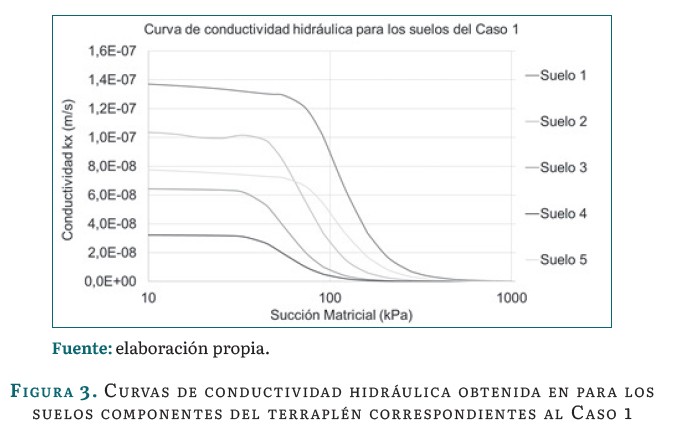
Caso 2: Permeabilidad obtenida empleando el modelo de Terzaghi a partir de la relación de vacíos inicial.
Para este caso, dada la variabilidad de los coeficientes que propone el método y que no se referencia límite inferior para los mismos en la bibliografía consultada, se estudiaron informes originales de presas de tierra recopilando los valores de la relación de vacío típica y la permeabilidad. Luego, a partir de estos valores, se estimó el coeficiente relacionado a los suelos arcillosos que conforman las terraplenes de presas de tierra. El coeficiente obtenido en estos casos fue de 5,4; el cual se empleó para estimar la permeabilidad empleando la formulación de Terzaghi para cada valor de relación de vacíos establecida. En la tabla 5 se muestran los resultados obtenidos de este análisis.
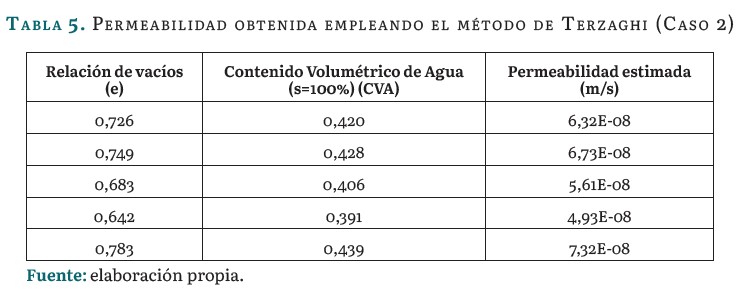
En la figura 4 se muestran las curvas de conductividad hidráulica correspondientes a los valores de permeabilidad de la tabla 5.
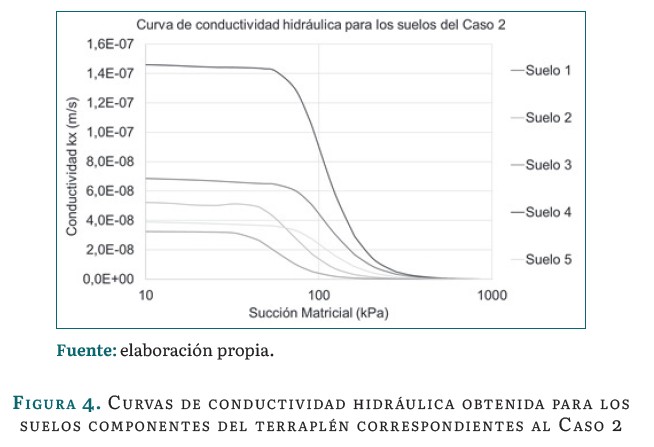
Caso 3: Permeabilidad obtenida empleando el modelo de Schlichter a partir de la relación de vacíos inicial.
Haciendo uso del procedimiento descrito y basándose en el método de Schlichter se muestran los resultados correspondientes en la tabla 6.

En la figura 5 se muestran las curvas de conductividad hidráulica correspondientes a los valores de permeabilidad de la tabla 6.
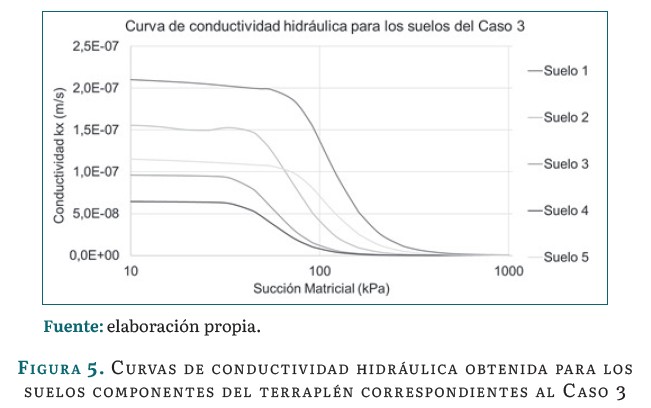
En todos los casos anteriores se establece una condición de anisotropía para el material del terraplén igual a . En cuanto a los materiales que conforman la base y el drenaje, el primero se establece como un lecho impermeable con alta resistencia y el segundo, como una grava con alta permeabilidad.
Se plantean tres intensidades de lluvia para un período de duración de cinco días medidos en intervalos de 24 horas. Las intensidades () definidas, a partir de relacionarlas con la permeabilidad (), se muestran en la tabla 7.
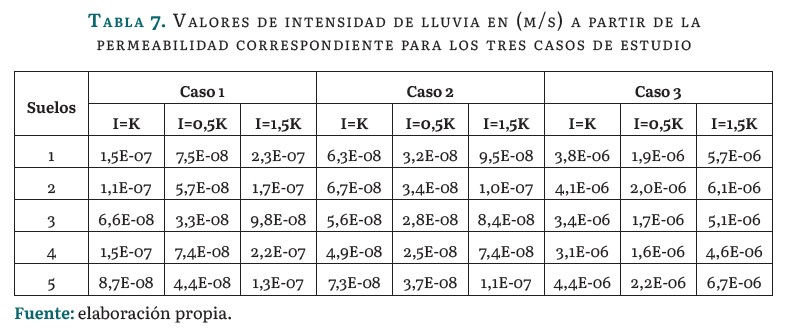
La combinación de todos los elementos expuestos previamente permite establecer un total de 45 modelos numéricos para, con el análisis posterior de los mismos, arribar a las conclusiones definitivas de la presente investigación.
RESULTADOS Y DISCUSIÓN
En la figura 6 se muestra el resultado obtenido en la modelación numérica de la lluvia sobre el talud aguas abajo.
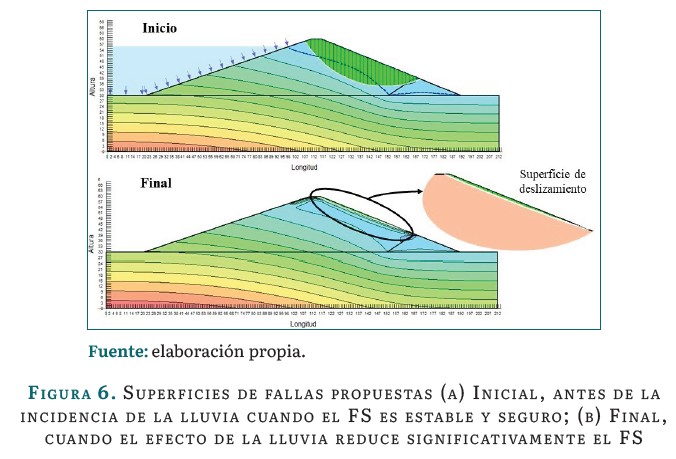
En la figura 6 (a) se observa cómo el modelo numérico propone una posible superficie de deslizamiento crítica de tipo profunda donde el FS es estable y seguro. Sin embargo, tras el período de lluvia analizado, en algunos casos aparece la superficie de falla propuesta en la figura 6 (b), donde esta se convierte en una superficie de falla de tipo superficial y el FS pasa a un estado de fallo.
En la figura 7 se muestran los resultados correspondientes al comportamiento del factor de seguridad para los cinco suelos estudiados, teniendo en cuenta que para los tres casos establecidos entre la permeabilidad y el contenido volumétrico de agua.
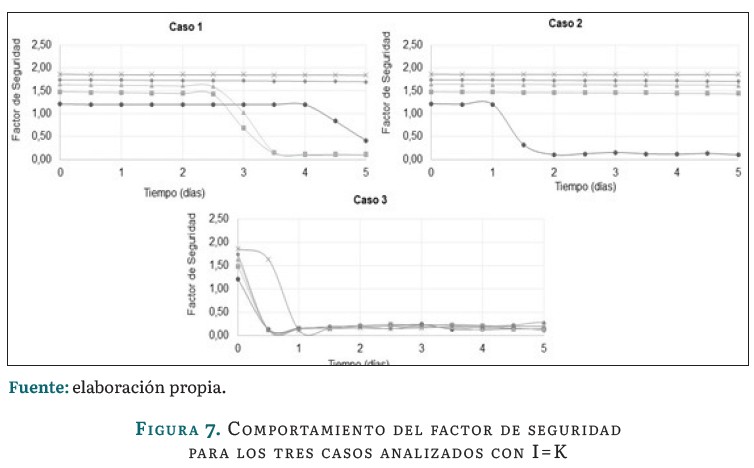
En la figura 7 se evidencia que, para el Caso 3, todos los suelos fallan durante las primeras 24 horas; esto ocurre debido a que la permeabilidad es la más alta, y también la intensidad de la lluvia asociada a ella. Sin embargo, para el Caso 2, las fallas se retrasan en todos los suelos considerados, notándose, incluso, que el suelo 2 no falla en ningún momento. Para el Caso 1, tres de los cinco suelos fallan antes de que termine el período analizado, no obstante, el suelo 2 mantiene un comportamiento similar al presentado para el Caso 2.
En la figura 8 se muestran los resultados correspondientes al comportamiento del factor de seguridad para los cinco suelos estudiados, teniendo en cuenta que para los tres casos establecidos entre la permeabilidad y el contenido volumétrico de agua.
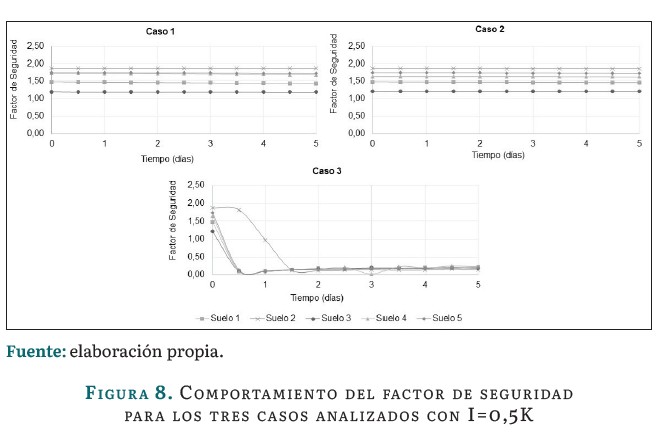
En la figura 8 se muestra que, de manera similar a cuando la intensidad de la lluvia es igual a la permeabilidad, cuando para el Caso 3, cuatro de los cinco suelos estudiados fallan antes de las 24 horas, y solo uno lo hace antes de las 48 horas. Para los casos 1 y 2 no se presentan las fallas en ningún momento de los cinco días de lluvia analizados.
En la figura 9 se muestran los resultados correspondientes al comportamiento del factor de seguridad para los cinco suelos estudiados, teniendo en cuenta que para los tres casos establecidos entre la permeabilidad y el contenido volumétrico de agua.
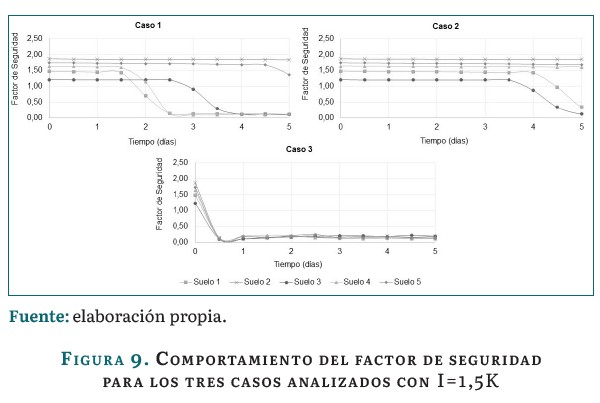
En la figura 9 se muestra que, al igual que para las intensidades de lluvia anteriores, el comportamiento para cada caso analizado es similar. Como se había visto previamente, para el Caso 3 todos los suelos fallan antes de transcurridas las primeras 24 horas. Para el Caso 2, las fallas se retrasan en todos los suelos considerados, presentándose a partir del día 4 las fallas de los suelos 1 y 3, los restantes suelos analizados no fallan. En el Caso 1, los suelos 1, 3 y 4 fallan a partir de las 48 horas de lluvia, mientras que el FS del suelo 5 comienza a decrecer a partir del cuarto día de lluvia y en el suelo 2 no ocurre la falla.
Existe una mayor similitud en el comportamiento del FS al relacionar los resultados obtenidos entre el Caso 1, cuando la permeabilidad es la obtenida para los suelos a partir de los estudios ingeniero-geológicos, y el Caso 2, al aplicar la ecuación de Terzaghi. Adicionalmente, se observa que, a mayor intensidad de lluvia, más rápido se produce la falla, independientemente de que esta haya sobrepasado el valor de permeabilidad del suelo estudiado.
Luego, se realiza un estudio del comportamiento suelo a suelo para los cinco materiales definidos, teniendo en cuenta las tres intensidades de lluvia establecidas y los tres casos de estudio planteados. Los resultados correspondientes para la relación se muestran en la figura 10.
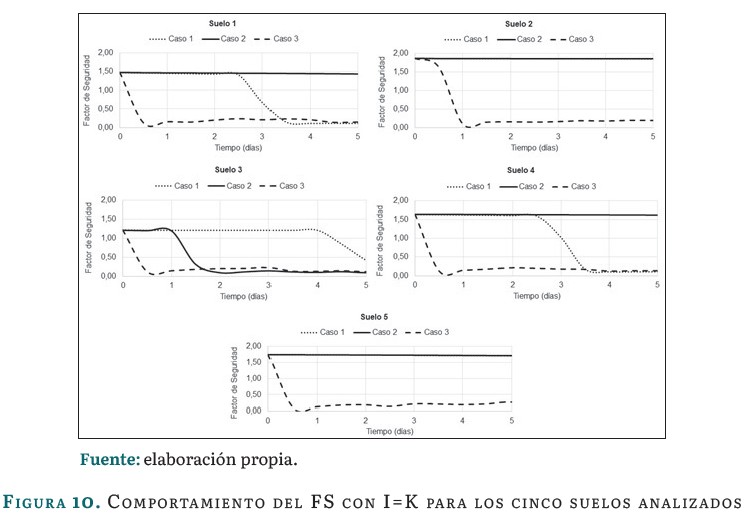
En la figura 10 se muestra el comportamiento del FS para cada suelo, considerando las tres relaciones de permeabilidades establecidas teniendo en cuenta que I=K. En los cinco suelos, el FS para el Caso 3 se reduce a mayor velocidad que para los restantes casos estudiados. Esto propicia que, para los cinco suelos, la falla ocurra antes de las primeras 24 horas. Puede notarse que el orden de ocurrencia de la falla se debe al valor de permeabilidad, a mayor permeabilidad, más rápido el tiempo en el que ocurre esta. Para el Caso 1, todos los suelos fallan a partir de las 72 horas de lluvia, excepto los suelos 2 y 5. Para el Caso 2, ninguno de los suelos falla, excepto para el suelo 3, en el cual el orden de falla se invierte; esta peculiaridad se debe al valor de la permeabilidad en cada caso.
Los resultados correspondientes a este análisis para la relación I=0,5K se muestran en la figura 11. Para este caso, todos los suelos presentan patrones de comportamiento similares al mostrado cuando I=K, aunque las fallas demoran más en producirse, pues la intensidad de la lluvia es mucho menor que la permeabilidad saturada en cada caso.
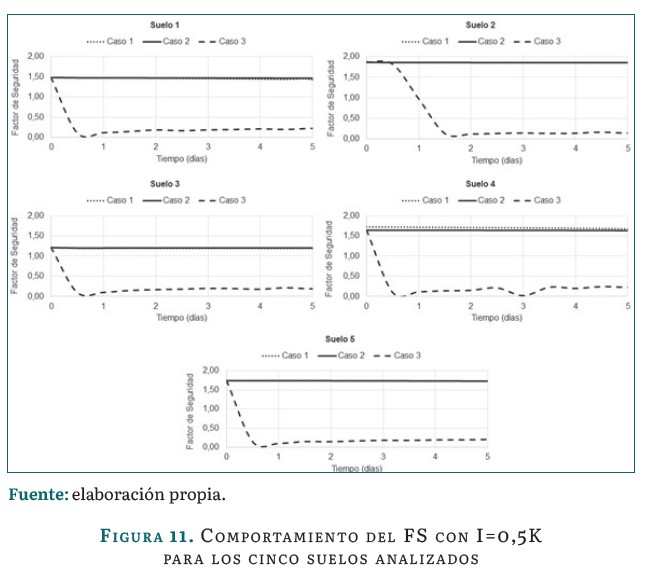
Los resultados correspondientes a este análisis para la relación I=1,5K se muestran en la figura 12.
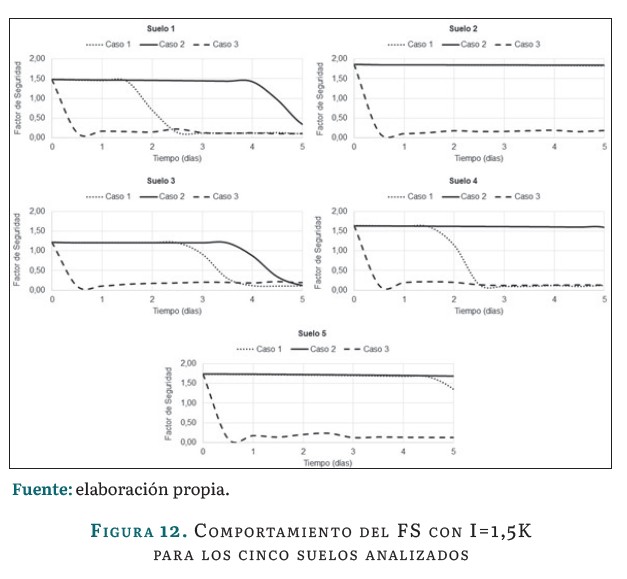
En la figura 12 se muestra, para todos los casos, un decrecimiento marcado del FS. Este comportamiento está asociado directamente a la intensidad de lluvia, que en este caso es la mayor de las tres relaciones planteadas. Por otro lado, el orden de ocurrencia de las fallas se mantiene, dado que este depende de los valores de permeabilidad, fallando primero el de permeabilidad más alta y por último el de menor permeabilidad.
CONCLUSIONES
La lluvia modelada con 5 días de duración continua afecta el comportamiento del FS asociado al talud aguas debajo de presas de tierra, observándose que su efecto produce una falla superficial para la geometría y todos los casos analizados, obteniéndose FS inferiores a 1, lo que denota que el talud se desliza.
Con el empleo del modelo de [10], que se basa en la granulometría del material para la obtención de la curva característica, y el modelo de [13], para la obtención de la curva de conductividad hidráulica, se observan resultados compatibles con lo observado en la práctica y la literatura, respecto a la inclusión del suelo parcialmente saturado en los análisis de estabilidad de taludes en presas de tierra.
A partir del análisis de los tres casos de estudio establecidos entre la permeabilidad y la relación de vacíos, se recomienda el empleo del método de Terzaghi para estimar la permeabilidad del suelo, cuando no se cuentan con los datos de laboratorio. Este método presenta los resultados más similares a los presentes en las obras construidas. Los resultados más alejados del comportamiento estructural de las presas fueron los obtenidos mediante el método de Schlichter.
Es posible establecer una relación entre el tiempo de falla, el método de estimación de la permeabilidad y el FS para la intensidad de lluvia, observando que en el método de Schlichter los resultados son los más desfavorables, mientras que para el método de Terzaghi se obtienen los resultados menos conservadores. Para este último se observan los valores que más se asemejan a los apreciados en las obras de este tipo ya construidas, por lo que se recomienda el empleo de este método para la obtención de la permeabilidad a partir de la relación de vacíos de los suelos, si no se cuenta con los datos de laboratorio.
* Profesora asistente, Universidad Tecnológica de La Habana "José Antonio Echeverría" (CUJAE), Departamento de Estructuras, Cuba. Máster en Ingeniería Civil. Orcid-ID: https://orcid.org/0000-0001-8492-0928. isiflores92@gmail.com.
** Profesora instructora, Universidad Tecnológica de La Habana "José Antonio Echeverría" (CUJAE), Centro de Investigaciones Hidráulicas, Cuba. Orcid-ID: https://orcid.org/0000-0001-9608-0815. jacobodalys96@gmail.com.
***Ingeniera hidráulica especialista, Biocubafarma. Orcid-ID:https://orcid.org/0009-0004-2789-446X. garciamartinezsamdy@gmail.com.
****Profesor titular, Universidad Tecnológica de La Habana "José Antonio Echeverría" (CUJAE), Especialista en Instituto Nacional de Recursos Hidráulicos, Cuba. Doctor en Ciencias Técnicas. Orcid-ID: https://orcid.org/0000-0001-8613-6264. yoermes@civil.cujae.edu.cu.
*****Profesora titular, Universidad Tecnológica de La Habana "José Antonio Echeverría" (CUJAE), Departamento de Estructuras, Cuba. Doctora en Ciencias Técnicas. Orcid-ID: https://orcid.org/0000-0003-3072-8011. jenny@civil.cujae.edu.cu.
REFERENCIAS
[1] S. K. Vanapalli y F. M. O. Mohamed, "Bearing capacity and settlement behaviour of footings in an unsaturated sand", Int. J. GEOMATE, vol. 5, n°. 1, pp. 595-604, 2013. doi: 10.21660/2013.9.3k.
[2] J. A. Mendoza, "Influencia de las propiedades no saturadas del suelo en los análisis numéricos de flujo de agua y estabilidad de taludes" [En linea]. Universidad Nacional Autónoma de México, 2018. Diaponible en: http://journal.stainkudus.ac.id/index.php/equilibrium/article/view/1268/1127%0A. http://publicacoes.cardiol.br/portal/ijcs/portugues/2018/v3103/pdf/3103009.pdf%0A. http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0121-75772018000200067&lng=en&tlng=
[3] I. Flores, J. G. Tristá y Y. G. Haramboure, "Estabilidad de taludes durante un desembalse rápido en presas de tierra con suelos parcialmente saturados", Ingeniería y Desarrollo, vol. 38, n°. 1, pp. 13-31, 2020 [En línea]. Disponible en: http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0122-34612020000100013&lng=en&nrm=i so&tlng=es%0A http://www.scielo.org.co/scielo.php?script=sci_abstract&pid=S0122-34612020000100013&lng=en&nrm=iso&tlng=es
[4] D. G. Fredlund y H. Rahardjo, Soil Mechanics for Unsaturated Soils. John Wiley & Sons, 1993.
[5] M. Ahmadi-adli, N. Huvaj y N. K. Toker, "Rainfall-triggered landslides in an unsaturated soil: A laboratory flume study", Env. Earth Sci., vol. 76, p. 735, 2017. doi: 10.1007M2665-017-7049-z.
[6] J. Kim, Y. Kim, S. Jeong y M. Hong, "Rainfall-induced landslides by deficit field matric suction in unsaturated soil slopes", Environ. Earth Sci., vol. 76, p. 808, 2017. doi: https://doi.org/10.1007/s12665-017-7127-2.
[7] H.-F. Yeh, J. Wang, K.-L. Shen y C.-H. Lee, "Rainfall characteristics for anisotropic conductivity of unsaturated soil slopes", Environ. Earth Sci., vol. 73, pp. 8669-8681, 2015. doi: 10.1007M2665-015-4032-4.
[8] J. G. Tristá, "Estudio del comportamiento tenso-deformacional de suelos parcialmente saturados en Cuba", Universidad Central "Marta Abreu" de las Villas; Instituto Superior Politécnico "José Antonio Echeverría", 2015.
[9] L. M. Arya y J. F. Paris, "A Physicoempirical Model to Predict the Soil Moisture Characteristic from Particle-Size Distribution and Bulk Density Data", Soil Sci. Soc. Am. J., vol. 45, pp. 1023-1030, 1981. doi: https://doi.org/10.2136/sssaj1981.03615995004500060004x.
[10] M. Aubertin, M. Mbonimpa, B. Bussière y R. P. Chapuis, "A model to predict the water retention curve from basic geotechnical properties", Can. Geotech. J., vol. 1122, pp. 11041122, 2003. doi: 10.1139/T03-054.
[11] G. Torres, "Estimating the Soil-Water Characteristic Curve Using Grain Size Analysis and Plasticity Index", Universidad Estatal de Arizona, 2011 [En línea]. Disponible en: http://medcontent.metapress.com/index/A65RM03P4874243N.pdf%5Cn http://repository.asu.edu/attachments/56747/content/TorresHernandez_asu_0010N_10702.pdf.
[12] D. G. Fredlund y A. Xing, "Equations for the soil-water characteristic curve," Can. Geotech. J., vol. 31, n°. 4, pp. 533-546, 1994. doi: https://doi.org/10.1139/t94-061.
[13] D. G. Fredlund, A. Xing y S. Huang, "Predicting the permeability function for unsaturated soils using the soil-water characteristic curve", Can. Geotech. J., vol. 31, n°. 3, pp. 521-532, 1994. doi: 10.1139/t94-062.
[14] R. L. López, "Evaluación del coeficiente de permeabilidad efectivo en depósitos cuaternarios e implicancias en los diseños de presas alto andinas, casos Cusco y Apurimac", Universidad Nacional de San Agustín de Arequipa, 2018 [En línea]. Disponible en: https://repositorio.unsa.edu.pe/items/a7b1cea4-6eaf-4bbb-9593-8e1a973641bc
[15] N. R. Morgenstern y V. E. Price, "The analysis of the stability of general slip surfaces," Geotechnique, vol. 15, n°. 1, pp. 79-93, 1965. doi: https://doi.org/10.1680/geot.1965.15.1.79.