Artículo de investigación research report

http://dx.doi.org/10.14482/zp.32.372.218

cristianne butto zarzar

Universidad Pedagógica Nacional, Unidad Ajusco, Ciudad de México, México. Doctora en Ciencias con Especialidad en Matemática Educativa, Cinvestav, México.

Correo electrónico: cristianne@upn.mx Código ORCID: 0000-0001-8913-2832

Joaquín Delgado

Departamento de Matemáticas, Universidad Autónoma Metropolitana-Iztapalapa, Ciudad de México, México. Doctor en Ciencias (Matemáticas), Universidad Autónoma Metropolitana-Iztapalapa

Correo electrónico: joaquin.delgado.f@gmail.com Código ORCID: 00 00-0002-7316-6672

Como citar este artículo:

Gómez Urrutia, V. & Arellano Faúndez, O.(2019). Portafolio reflexivo: una propuesta para la enseñanza de la Metodología Cualitativa. Zona Próxima, 31, 90-33.

Recibido: 3 de junio de 2019
Aprobado: 17 de septiembre de 2019

RESUMEN

Se presenta un estudio sobre la identificación y el desarrollo del talento matemático en estudiantes de educación básica primaria y secundaria fundamentado en el Modelo de Enriquecimiento Escolar de Renzulli. La metodología usada fue de tipo mixto con diseño incrustado concurrente de modelo dominante. Las dos etapas del estudio consistieron en: a) detectar estudiantes con talento matemático en educación primaria básica y secundaria en lo que se refiere a los procesos de generalización; y b) diseñar y aplicar un programa de enriquecimiento extraescolar con estudiantes de educación primaria básica y secundaria en lo se que refiere a los procesos de generalización en ambiente eXpresser y Google Maps, así como en la hoja de cálculo Excel. El programa de enriquecimiento extraescolar mostró ser efectivo, pues los alumnos lograron transitar hacia un pensamiento multiplicativo.

Palabras clave: educación básica primaria, procesos de generalización, talento matemático.

ABSTRACT

A study on the identification and development of mathematical talent in elementary and secondary school students is presented and based on the Renzulli's School Enrichment Model. The methodology used was mixed type with concurrent embedded design of dominant model. The two stages of the study consisted of: (a) detecting students with mathematical talent in basic and secondary primary education in terms of generalization processes; and (b) designing and implementing an extracurricular enrichment program with students of basic and secondary primary education In terms of generalization processes in eXpresser and Google Maps environment, as well as in the Excel spreadsheet. The extracurricular enrichment program proved effective as the students managed to move towards multiplicative thinking.

Key words: primary education, generalization processes, mathematical talent.

Introducción

En esta sección se presenta un breve recuento histórico del tema de superdotación y talento (G&T, por sus siglas en inglés) desde la perspectiva de dos potencias en constante competencia por el liderazgo político y tecnológico mundial: Estados Unidos y Rusia (anteriormente la Unión Soviética), posteriormente presentamos algunas iniciativas propias de Latinoamérica y particularmente en México.

Los estudios de superdotación se remontan a 1860 cuando Galton publica Hereditary Genius, un estudio biográfico de cuatrocientos hombres británicos. El autor concluye que la inteligencia se deriva por herencia y selección natural. Binet y Simon, en 1905, desarrollan una serie de pruebas con el fin de separar a niños con inteligencia inferior de los normales, a fin de colocarlos en clases especiales. Lewis Terman, considerado el padre del movimiento para la educación de los superdotados, publica en 1921 la escala Stanford-Binet, realizando un estudio longitudinal amplio que incluyó a mil quinientos niños superdotados. En 1926, Leta Hollingwort publica la obra Gifted children: their nature and nurture, considerado el primer libro de texto en el tema de superdotación. Hollingwort forma la primera escuela Speyer en Manhattan para niños superdotados de siete a nueve años. A iniciativa de J. P. Guilford, en la conferencia inaugural de 1950 de la convención anual de la Asociación Norteamericana de Psicología (APA), se promueve la investigación sobre dotación y talento con objeto de definir con precisión el concepto. La Guerra Fría promueve la investigación e identificación de los estudiantes más brillantes y talentosos. El Reporte Marland (1971) fue una iniciativa legislativa que alentó a las escuelas a que definieran la superdotación de manera amplia. El reporte de 1983, A Nation at Risk da cuenta de los puntajes de los estudiantes más brillantes de los Estados Unidos y su incapacidad para competir con sus homólogos internacionales; el reporte recomienda el aumento de los estándares académicos y la promoción del plan de estudios adecuado para los alumnos dotados. La NAGC, en 1998, publica los "Estándares del Programa para Estudiantes Superdotados de Pre-K a Grado 12" a fin de proporcionar orientación en siete áreas clave para los programas dirigidos a estudiantes dotados y talentosos. A nation deceived: how schools hold back America's brightest students (2004) es un reporte publicado por el Centro Belin-Blank de la Universidad de Iowa, en el que se reportan estrategias de aceleración para estudiantes avanzados. En el 2006, la NAGC publica estándares nacionales de educación dirigidos a programas de preparación de maestros y estándares de conocimiento y habilidades en educación de superdotados para todos los maestros. Las normas se revisaron en el 2013.

En el bloque socialista los precursores de la versión moderna del sistema de G&T en Rusia se remontan al siglo XIX (Grigorenko, 2017), con las primeras "Olimpiadas de la Mente de los Estudiantes." Cuando reaparecieron en la década de 1930, se hicieron muy populares y fueron una de las características más conocidas del sistema educativo soviético. Boris Delone, conocido matemático y académico, desempeñó un papel crítico en la reintroducción de estas olimpiadas en la educación rusa-soviética en 1934. Las Olimpiadas de Matemáticas se unieron con las Olimpiadas de Física y Química en 1938, pero fueron interrumpidas por la Segunda Guerra Mundial y solo se retomaron a fines de los años cincuenta. A fin de mantener la afluencia de alumnos dotados, además de las olimpiadas se establecieron cuatro internados especializados para niños y adolescentes con conocimientos en matemáticas y ciencias en Moscú, Leningrado, Kiev y Novosibirsk, en 1963. Estas escuelas reclutaron estudiantes por medio de las olimpiadas, pero debido a la lejanía de algunas comunidades, algunos niños se correspondían con estas escuelas para recibir y enviar tareas. Este modelo de educación a distancia se mejoró con el establecimiento, en 1970, de la revista Kvant, dirigida a niños en edad escolar, la cual publicó materiales educativos, interpretó descubrimientos científicos para niños y diseminó problemas complejos a fin de que los resuelvan y los devuelvan a la revista. La versión en inglés, Quantum, se publicó bimestralmente como una revista de la NSF en cooperación con Springer-Verlag New York (Ushakov, 2010). Vale la pena hacer una observación especial con respecto a la utilización de pruebas psicológicas en el sistema educativo ruso. El uso de pruebas psicológicas en el contexto de la educación se prohibió, de manera explícita, en 1936 (Comité Central del PCUS, citado en Grigorienko, 2017). En consecuencia, el uso de pruebas estandarizadas en Rusia, en el contexto de los programas G&T, es muy limitado. Sin embargo, los bajos resultados de las pruebas no excluyen la presencia de dones intelectuales ni la posibilidad de que estos dones se desarrollen en el futuro. Por tanto, se recomienda que estas pruebas se utilicen para fines de inclusión, mas no de exclusión; esta recomendación se conoce como el uso de "criterios positivos" de las pruebas. En resumen, la educación de niños G&T en Rusia está estrechamente vinculada a su identificación inicial y su demostración recurrente de alto rendimiento, es decir, la justificación repetida de su estado G&T.

Iniciativas de atención a estudiantes G&T

La atención de estudiantes con habilidades excepcionales en matemáticas es tema de interés también para otros sistemas educativos. En España, a partir de 1998, se desarrolló el programa "Estímulo del talento matemático " (Estalmat), diseñado para la detección, la orientación y la estimulación de manera continua del talento matemático de estudiantes de doce a trece años a lo largo de dos cursos, por medio del enriquecimiento curricular en cursos diseñados por especialistas en el tema, en las sesiones que se realizan una vez por semana (Fernández y Pérez, 2011). Los resultados iniciales del proyecto demostraron que los niños participantes de este programa alcanzan un mayor grado de conocimiento y creatividad en diferentes aspectos de las matemáticas, y cómo su participación en el proyecto fortaleció y reforzó sus actitudes y aptitudes hacia las matemáticas en diferentes áreas.

En Colombia, la Universidad Sergio Arboleda desarrolla el proyecto "Semicírculo", el cual inicia con sabatinos de treinta horas para niños de quinto a séptimo grado, entre los diez y los trece años, para la identificación de talentos en cursos en los que se observa la argumentación, el trabajo en equipo, la iniciativa y la actitud hacia el fracaso. Algunos de estos alumnos se promueven a la segunda etapa con cursos de sesenta horas para niños de noveno a once grado en los que se trabajan teorías matemáticas elementales con mayor profundidad, como, por ejemplo, geometría, fundamentos de matemáticas e introducción al cálculo. En una tercera etapa los alumnos seleccionados se relacionan con pares académicos de la universidad. Los autores afirman que el mejor ambiente para desarrollar tal proyecto es el ambiente universitario, y han realizado un seguimiento biográfico de la vida académica de los egresados (Núñez, Gómez-Bermeo y Cortés, 2011; Núñez, Pérez, Luque y Arévalo, 2004).

En Chile se desarrolló el programa "Búsqueda y desarrollo de talentos matemáticos" de la Pontificia Universidad Católica de Chile, que inició en 1993 y se mantuvo vigente hasta el año de 2001. El objetivo fue identificar estudiantes con talento matemático (en dos ocasiones, 1993 y 1998) con una prueba de matemáticas y desarrollar el talento matemático en estudiantes que se encontraran entre los nueve y los diez años de edad. En el programa se impartían clases de matemáticas diseñadas por expertos en el tema; este programa piloto sirvió de base para el "Programa de Estudios y Desarrollo de Talentos de la Universidad Católica" (Penta-UC) y que buscó desarrollar el talento en diversas áreas. (Benavides, Ríos y Marshall, 2004). Derivado de este trabajo, se han realizado programas de posgrado para docentes que trabajan en educación, especialmente con estudiantes con talento, así como tambien se han desarrollado otro tipo de actividades, como seminarios para la formación de docentes y talleres para padres; también se han desarrollado investigaciones sobre la pertinencia de atender a esta población.

En México, la Secretaría de Educación Pública (SEP, 2011) implementó, en 1986, el programa de "Atención a Niños y Jóvenes con Capacidades y Aptitudes Sobresaliente" (CAS). Esta propuesta se fundamentó en un programa de enriquecimiento curricular mediante actividades como, por ejemplo, "Filosofía para niños" y "Desarrollo de la inteligencia a través del Arte". El programa estuvo vigente a nivel nacional hasta 1993 y, luego, con la reorganización de la SEP, se originaron las secretarías de educación estales y la atención de los alumnos CAS se transfirió a los estados que propusieron diversas estrategias para tal finalidad. En la actualidad se han desarrollado otros programas para el desarrollo del talento científico y matemático, por ejemplo, el programa "Adopte un talento" (Pauta), que inició actividades en el 2007 y lo financia el Consejo Nacional de Ciencia y Tecnología (Conacyt) de México, con el apoyo del Instituto de Ciencias Nucleares, el Instituto de Biotecnología y la Dirección General de Divulgación de la Ciencia de la Universidad Nacional Autónoma de México cuenta con sedes en distintos estados del país. De acuerdo con De la Torre, Del Valle, Carpinteyro y Mijangos (2017), el programa se basa en una propuesta constructivista y se enfoca, principalmente, en el desarrollo del talento científico en niñas, niños y adolescentes por medio de talleres de ciencia, vinculación con investigadores de diversas universidades y además realizan acompañamiento a padres de familia.

El proyecto de Círculos matemáticos, del Instituto de Matemáticas de la UNAM, México, tiene como objetivo generar un espacio de convivencia entre la comunidad matemática y los estudiantes del sistema educativo nacional. Una de las finalidades es compartir el gusto y el entusiasmo hacia las matemáticas, así como promover el razonamiento abstracto. Las actividades que se desarrollan en dicho proyecto se realizan por medio de talleres lúdicos que profundizan en contenidos que no aparecen en los planes y los programas de estudio de México. Los programas de círculos matemáticos se originaron en la Unión Soviética y, posteriormente, se extendieron a Europa del Este; en décadas recientes han sido desarrollados en EE. UU. Este proyecto se inició en 2016, en el Instituto de Matemáticas de la UNAM con convocatoria abierta desde el 2017, y ha sido de gran ayuda para los alumnos que participaron en el programa.

En la Universidad Autónoma Metropolitana Unidad Iztapalapa (UAM-I), Ciudad de México se desarrolla el Instituto Carlos Graef Jóvenes hacia las Ciencias y las Ingenierías, es un programa que en su origen fue orientado a captar el interés de jóvenes de nivel bachillerato por estudiar las carreras de física y matemáticas; y luego se amplió hacia las ciencias (física, matemáticas y química) y las ingenierías (computación, procesos e hidráulica, química y biomédica). En el programa colaboran científicos profesionales dedicados a la docencia, la investigación y la difusión de la ciencia, de los departamentos de Física y de Matemáticas, además de otras ramas de la ingeniería. En este proyecto se realizan talleres y conferencias sobre ciencias exactas y la implicación de estas en el nuevo conocimiento.

En el Centro de Investigación en Matemáticas A. C., en Guanajuato (CIMAT), México, se desarrolla un programa desde el 2011, se denomina "Matemorfosis" (término compuesto de las palabras Matemáticas y metamorfosis, "cambio" o "transformación") y tiene como objetivo acercar las matemáticas a los niños, los jóvenes y el público en general, de un forma lúdica. A partir del proyecto "Matemorfosis" se crea la Coordinación de Divulgación en el CIMAT, desde donde se planean diversas actividades dirigidas a promover la cultura matemática en el estado. Entre estas actividades se encuentran ciclos de conferencias, talleres de divulgación, festivales de ciencias, una olimpiada de matemáticas y la formación de divulgadores de ciencias, entre otras.

Las iniciativas mencionadas no tienen por principio atender a alumnos con altas habilidades, excepto el programa de olimpiadas de matemáticas del CIMAT, sino hacer atractivas las matemáticas y estimular su reflexión.

El proyecto TAMME UPN-Ajusco

El proyecto "Talento matemático mexicano" (TAMME) es un programa de enriquecimiento ex-traescolar para el desarrollo del talento matemático con estudiantes, profesores y padres de familia de educación primaria y secundaria de la Ciudad de México y el estado de México. El programa de enriquecimiento se desarrolla por medio de actividades Tipo I según el modelo de Renzulli (2008). De forma simultánea, se ofrecen talleres vivenciales para padres de familia, impartidos por un profesor y un profesional psicoterapeuta de la UPN-Ajusco. Las sesiones se realizan de manera quincenal los días viernes y sábado de manera alternada, de dos horas y media aproximadamente en las instalaciones de la UPN-Ajusco.

Marco teórico

El Modelo Enriquecimiento Escolar (SEM)

El Modelo de Enriquecimiento Escolar (SEM, por sus siglas en inglés, School Wide Enrichment Model) se originó a partir del Modelo de la Triada de Enriquecimiento de Renzulli y Reiss (1985) y Renzulli (2008), y se diseñó con la intención de fomentar y desarrollar la productividad creativa. En el SEM el talento se representa por tres anillos que definen comportamientos talentosos más que individuos talentosos. Estos tres componentes se interrelacionan:

El comportamiento talentoso consiste de comportamientos que reflejan la interacción entre tres cúmulos de tres rasgos humanos-habilidad promedio superior, altos niveles de compromiso de tareas, y altos niveles de creatividad. Los individuos capaces de desarrollar un comportamiento talentoso son los que poseen o son capaces de desarrollar este conjunto complejo de rasgos humanos y aplicarlos a un área potencialmente valiosa de la actuación humana. Las personas que manifiestan o son capaces de desarrollar una interacción entre los tres cúmulos requieren de una variedad de oportunidades de educación y servicios que no son provistos ordinariamente mediante programas de instrucción regular.

El modelo de triada consiste en tres tipos de actividades de enriquecimiento clasificadas en tipos I, II y III. El enriquecimiento del Tipo I se puede dar a grupos generales o estudiantes que hayan expresado interés en el tópico del área. El enriquecimiento del Tipo II, usualmente, se otorga a grupos de estudiantes en sus clases o en programas de enriquecimiento. Incluye el desarrollo de: a) pensamiento creativo y resolución de problemas, pensamiento crítico y procesos afectivos; b) una gran variedad de habilidades específicas de cómo aprender; c) habilidades en el uso apropiado de materiales de referencia de nivel avanzado; y d) comunicaciones escritas, orales y visuales. El enriquecimiento de Tipo III involucra a estudiantes que se interesan en proseguir en un área de su elección y están dispuestos a comprometerse con el tiempo necesario para la adquisición de contenidos avanzados y el entrenamiento de procesos en los que ellos asumen el papel de indagador de primera mano. El SEM contiene otras componentes que se ilustran en la Figura 1, en cuyo frente se encuentre la triada y como dimensiones adicionales el currículum regular, los cúmulos de enriquecimiento y el continuo de servicios especiales. Los recursos de implementación están formados por los recursos institucionales y materiales sobre los que se concreta el modelo en una escuela particular.

Figura 1. Modelo de enriquecimiento escolar de Renzulli (SEM)

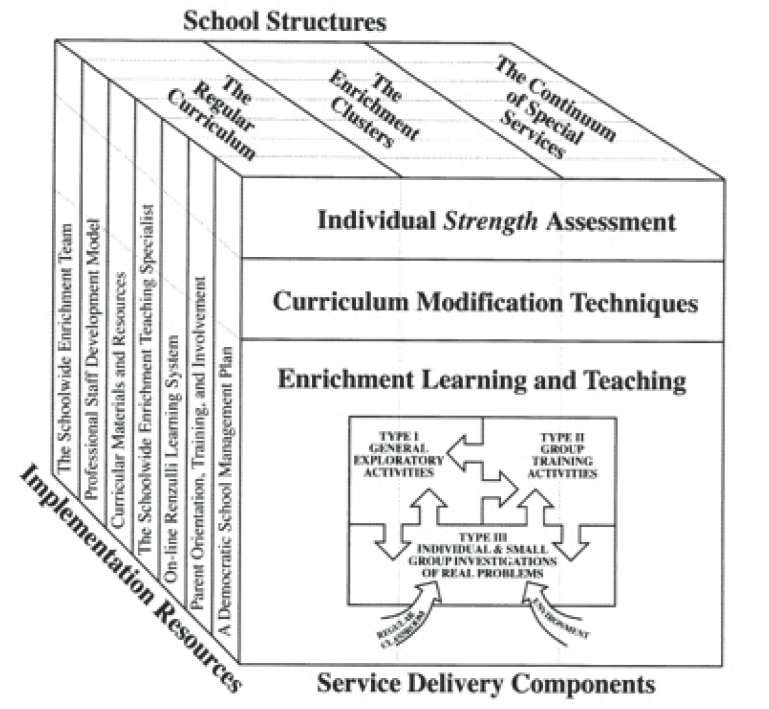
Fuente: Elaboración propia

A partir de 2017 se ha implementado otra componente del SEM basado en la web: el Renzulli Learning©. Este consta, esencialmente, de tres módulos: el "Perfilador", en el que, a partir de preguntas de diversas categorías, se determina un reporte sobre intereses, estilos de aprendizaje y de expresión; una vez los estudiantes completan sus perfiles, tienen acceso a sus propias bases de datos personalizadas en el módulo de "Actividades de enriquecimiento" y, finalmente, el "Portafolio", el cual permite a los estudiantes mostrar su trabajo académico y mantener un historial de todas las actividades de aprendizaje.

Esta investigación presenta resultados de un programa de enriquecimiento extracurricular para el desarrollo del talento matemático con estudiantes de educación primaria básica y secundaria de escuelas de la Ciudad de México y el estado de México bajo el marco teórico de Renzulli. El programa se realiza por medio de talleres de matemáticas dirigidos a estudiantes y talleres dirigidos a padres de familia con el fin de mejorar la comunicación y la relación con los hijos.

Las actividades que se describen en el programa de enriquecimiento extracurricular corresponden al trabajo realizado con los procesos de generalización y el pensamiento computacional.

Los procesos de generalización

Los contenidos matemáticos que se trabajan en el programa de enriquecimiento para el grupo de primaria son temas que están interconectados conceptualmente y hacen el tránsito de los problemas de estructura aditiva o multiplicativa al pensamiento algebraico. De acuerdo con Butto y Delgado (2012), este contenido se encuentra en el curriculum mexicano y es una etapa que se caracteriza por la transición de la educación primaria a la secundaria. Según estos autores, los procesos de generalización son un tema importante de investigación y diversos autores lo consideran una ruta de acceso al pensamiento algebraico temprano, como, por ejemplo, Bednardz, Kieran y Lee (1996), o Butto, Delgado y Bazán (2018), quienes reconocen cuatro acercamientos a la enseñanza del álgebra: a) la generalización de patrones numéricos y geométricos y de las leyes que gobiernan las relaciones numéricas; b) la modelización de situaciones matemáticas y de situaciones concretas; c) el estudio de situaciones funcionales; y d) la resolución de problemas y ecuaciones. En este estudio se trabaja la generalización de patrones numéricos y geométricos, así como de las leyes que gobiernan las relaciones numéricas, como una vía para acceder al pensamiento algebraico temprano.

La utilización de patrones en la enseñanza de las matemáticas es pertinente por lo menos por dos razones: primero, porque el mundo en que vivimos contiene patrones y regularidades; segunda, porque los patrones están presentes en las matemáticas y la habilidad para reconocerlos contribuye a llegar, de manera intuitiva, a fórmulas y relaciones que pueden utilizarse en matemáticas, como, por ejemplo, en álgebra.

Según Mason, Graham, Pimm y Gower (1985), el uso de patrones es importante para el pensamiento matemático y algebraico. La generalización en álgebra es algo primario hacia la abstracción matemática y puede desarrollarse a partir del trabajo con patrones o regularidades, de modo que beneficie su articulación en situaciones diarias y escolares que posteriormente ayudarán al pensamiento algebraico. En consecuencia, a fin de aprender el lenguaje algebraico es importante que el alumno tenga algo que comunicar; para eso necesita percibir un patrón o una regularidad y, después, intentar expresarlo y comunicarlo a alguien. Para Mason et al. existen cuatro etapas que permiten trabajar la generalidad en el salón de clases: percibir un patrón, expresarlo, registrarlo y probar la validez de las fórmulas.

De acuerdo con Castro, Rico y Castro (1995), toda situación repetida con regularidad involucra un patrón. Estos pueden formarse a partir de un núcleo que genera situaciones y, en algunas ocasiones, el núcleo se repite y en otros crece de manera regular. La matemática descubre patrones en los números, en la computadora, en el espacio y en la imaginación. Las teorías matemáticas ayudan a comprender las relaciones entre los patrones y sus estructuras, con el objetivo de explicar y predecir fenómenos que fijan un patrón.

El trabajo con patrones lo recomienda también, en los estándares curriculares y de evaluación, la National Council Teacher of Mathematics (NCTM, 1989), cuyo documento recomienda el uso de patrones desde muy temprana edad (lo equivalente a la enseñanza preescolar), extensible hasta los grados superiores, pues señala que el trabajo con los procesos de generalización puede, inicialmente, desarrollarse de forma intuitiva, al observar la regularidad y al desarrollar un trabajo con patrones. Regianni (1994) comenta que procesos de generalización es un término utilizado en matemáticas para indicar el paso de lo particular a lo general y observar la generalidad en casos particulares.

Objetivos

Los objetivos son:

■ Detectar estudiantes con talento matemático en educación primaria básica y secundaria en lo que se refiere a los procesos de generalización y el pensamiento computacional.

■ Diseñar y aplicar un programa de enriquecimiento extraescolar con estudiantes de educación primaria básica y secundaria con respecto a los procesos de generalización y el pensamiento computacional en entornos digitales de aprendizaje.

Escenario y participantes

Participaron del estudio ciento veintiséis alumnos de cuarto, quinto y sexto grado de primaria básica y primero y segundo grado de secundaria de escuelas públicas de la Ciudad de México y del Estado de México, con edades entre los nueve y los doce años, en el proceso de evaluación. Se seleccionó una muestra de cuarenta y seis estudiantes para el programa. Los estudiantes asisten a talleres de matemáticas que se llevan a cabo fuera de la escuela.

Localización del programa de talento matemático tamme

El programa se realiza en las instalaciones de la Universidad Pedagógica Nacional, Unidad Ajusco, de la Ciudad de México. Los talleres se imparten los días viernes y sábados, cada quince días, con una duración de dos horas, aproximadamente. Los estudiantes provienen de un nivel socioeconómico bajo.

Para la realización de los talleres dirigidos a los estudiantes, a los padres de familia y a los docentes se cuenta con los siguientes espacios:

■ Un aula por cada grupo de alumnos de primaria básica.

■ Aula de informática para los estudiantes de secundaria.

■ Sala para los talleres de padres de familia.

■ Patios.

Características del programa de talento matemático

El proyecto tiene por objetivo despertar la curiosidad científica y el desarrollo del talento matemático. Se trabajan actividades del Tipo I, de acuerdo con el modelo de Renzulli y Reiss (2008), por medio de talleres de matemáticas dirigidos a los estudiantes de educación primaria básica y secundaria. Además, se imparten talleres para los padres de familia de manera simultánea a los talleres para docentes.

La intervención orientada al desarrollo del talento matemático se centra en la realización de actividades Tipo I que tratan actividades y contenidos con diversos materiales materiales didácticos. En este sentido, se destaca el trabajo para restaurar la motivación y el nivel de rendimiento, así como el entrenamiento de habilidades comunicativas y de interacción social entre los estudiantes como una manera de aprender matemáticas.

Metodología

El corte del estudio de esta investigación fue mixto. Como referencia, Tashakkori y Teddlie (2009, citados en Hernández et al., 2014) mencionan que el método mixto es un tipo de diseño de investigación que emplea las metodologías cuantitativa y cualitativa en el tipo de preguntas de investigación, recolección de datos, procedimientos de análisis e hipótesis. Se utilizó un diseño anidado o incrustado concurrente de modelo dominante (DIAC) (Hernández et al., 2014). En el DIAC se recolectan de forma simultánea datos cuantitativos y cualitativos, y difiere de otros diseños mixtos, pues aquí un método predomina sobre el otro. Un método dirige el proyecto (en esta investigación predomina el cualitativo). El método con menor prioridad es anidado o incrustado dentro del método principal. El método secundario (en este caso el método cuantitativo) responderá a diferentes preguntas de investigación respecto al método principal. Este diseño ofrece una visión amplia del fenómeno estudiado, con la diferencia de que se usará un solo método; algunos datos cualitativos se pueden incorporar a fin de describir el objeto de estudio y obtener mayor información, lo cual no ocurre si solo se cuantificara, o en una situación contraria. En este diseño se recolectan, de manera simultánea, datos cuantitativos y cualitativos.

Los datos cuantitativos y cualitativos se comparan en la fase de análisis. En este caso, la primera parte del estudio la componen la información obtenida mediante el cuestionario de procesos de generalización, la escala de estilos de aprendizaje y la escala de apoyo familiar; en la fase de análisis se categorizaron las respuestas dadas por los alumnos con el propósito de observar las estrategias de resolución de problemas que utilizaron. Con los datos de las escalas se buscó observar la relación entre apoyo familiar y estilo de aprendizaje.

Descripción de las etapas del estudio

Etapa 1

En esta etapa se busca detectar estudiantes con talento matemático en educación primaria básica y secundaria, en lo que se refiere a los procesos de generalización.

A fin de detectar a los estudiantes con talento matemático en educación primaria básica y secundaria se utilizaron los siguientes instrumentos.

■ Cuestionario sobre procesos de generalización de Butto et al. (2018). El instrumento contiene cuatro tipos de preguntas: sucesión aritmética creciente y decreciente, sucesión geométrica, relación cuadrática y variación de número general, los cuales aparecen en la Tabla 1.

La entrevista clínica individual. Tiene como objetivo indagar sobre los procedimientos y las estrategias que utilizaron los niños para responder el cuestionario de procesos de generalización.

Cuestionario de estilos de aprendizaje (Alonso, Gallego y Honey, 2007). Se implemento con el fin de identificar el estilo de aprendizaje de los alumnos. Estuvo conformado por ochenta ítems agrupados en grupos de veinte cada uno, de acuerdo con los estilos de aprendizaje, clasificados en activo, reflexivo, teórico y pragmático. El alumno responde si está de acuerdo o en desacuerdo con la afirmación que se le presenta.

Escala de apoyo familiar de Bazán, Sánchez y Castañeda (2007). Tiene como finalidad obtener información relacionada con el apoyo que los padres brindan a sus hijos en las materias de español y matemáticas. Existen dos versiones del cuestionario: una dirigida a los padres y otra para el alumno, los cuales utilizan los mismos indicadores y las mismas preguntas (varía solo la forma de plantearlas). El cuestionario consta de diecinueve reactivos, distribuidos en cuatro dimensiones: 1) asistencia o apoyo en tareas escolares; 2) tiempo y espacio proporcionado para el estudio; 3) comunicación regular con los docentes y los directivos; y 4) repaso y evaluación; se contestan de forma separada para las materias "Español" y "Matemáticas", en una escala Likert con cinco opciones que miden la frecuencia de las conductas analizadas: a) nunca, b) casi nunca, c) algunas veces, d) casi siempre, y e) siempre, con excepción de uno de los ítems (tiempo dedicado por los padres al apoyo en las tareas escolares). Los resultados se ofrecen en un rango de valores entre 0 y 4 que se pueden interpretar, según los autores, como un indicador de la percepción sobre la frecuencia con la que los padres desarrollan cierto tipo de comportamientos de apoyo a sus hijos (los valores mayores indican una frecuencia mayor). De igual forma, se calcula un promedio general para cada una de las cuatro dimensiones del apoyo.

■ Nominación de compañeros y profesor. Técnica mediante la cual el profesor del grupo y los compañeros nombran a un compañero que ellos consideran se destaca en el área de matemáticas.

■ Calificaciones de matemáticas. Se consideraron las calificaciones de los estudiantes en esta disciplina como un indicador para el talento matemático.

Etapa 2

El programa de enriquecimiento extraescolar con estudiantes de educación primaria básica y secundaria, en lo que se refiere a los procesos de generalización con actividades en lápiz y papel, micromundo eXpresser, Google Maps y la hoja de cálculo Excel.

El programa de enriquecimiento extracurricular tiene como objetivo desarrollar el talento matemático de los estudiantes. En esta etapa se diseñaron actividades de enriquecimiento Tipo I, según la propuesta de Renzulli. Los estudiantes trabajaron en los talleres de matemáticas para primaria básica y secundaria.

En las actividades de generalización, en el grupo de primaria básica, que se describen a continuación, se hace uso del micromundo eXpresser, diseñado con el propósito de apoyar la construcción de patrones gráficos y su generalización mediante fórmulas aritméticas que contienen cantidades que pueden cambiarse al asumir el papel de las variables.

■ Talleres para estudiantes de educación primaria básica

Los estudiantes trabajaron en parejas, primero en actividades con lápiz y papel, y luego en actividades en eXpresser, acompañados de hojas de trabajo en cinco sesiones con duración de cincuenta minutos cada una. Se ofreció una breve exposición que explica cómo funciona eXpresser, y se leyó una de las hojas de trabajo a fin de indicar cómo sería el trabajo. Los contenidos matemáticos de las sesiones se resumen en la Tabla 2.

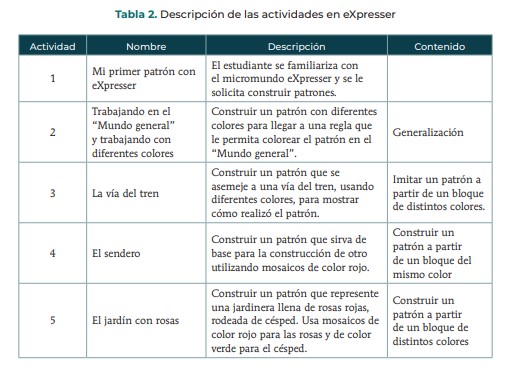
Utilizamos el eXpresser como un software con el fin de trabajar problemas que se refieren a los procesos de generalización, como, por ejemplo, los que se exponen a continuación.

El micromundo eXpresser

El término micromundo lo introdujo Seymour Papert como "un subconjunto de realidad o una realidad construida cuya estructura coincide con la de un mecanismo cognitivo dado para proporcionar un entorno donde este último pueda operar de manera efectiva". Uno de los primeros ejemplos fue Logo y sus variantes como, por ejemplo, el módulo "Turtle" en el lenguaje de programación Python. Otros ejemplos incluyen programación y robótica como Lego Mind Storms© o Drone Lego©. El micromundo eXpresser fue un proyecto del Grupo Migen, una plataforma de uso específico diseñada en Java que proporciona a los estudiantes un modelo para la generalización, de acuerdo con Geraniou, Mavrikis, Noss y Hoyles (2009). En eXpresser, los niños pueden construir patrones utilizando mosaicos y colores, así como encapsularlos en forma de bloques que pueden reproducirse de manera repetida y proporcionarle las reglas de colocación en las direcciones horizontal y vertical, así como cuántas veces repiten el bloque. Dada su sencillez y el enfoque hacia los procesos de generalización, se seleccionó como el ambiente de trabajo que se detalla más adelante. El micromundo contiene dos ventanas: "Modelo computacional" a la izquierda y "Mi modelo" a la derecha. En el ejemplo de la Figura 4, "Mi modelo" consiste en un patrón formado por un bloque que se repite tres veces, en el que el bloque (una flor) se compone de seis celdas rojas, dos verdes y dos amarillas. En la ventana de "Propiedades", la celda en rosa está desbloqueada y representa una variable, en este caso el número de veces que se repite el bloque; solo hasta que esta variable se usa de manera correcta para calcular el número total de celdas de cada color –como lo muestran las fórmulas bajo la pregunta "¿cuántas tejas?"– el patrón en el "Modelo computacional" se ilumina. El estudiante puede entonces dejar correr la simulación para verificar sus fórmulas. Nótese que cuando el modelo ha sido generalizado, en el sentido de que el total de tejas de cada color se calculan en términos de la variable libre (número de veces en el ejemplo), el "Modelo general" se ilumina, "Mi modelo" se encuadra con un borde magenta y ambos corren de manera asíncrona e independiente. De esta manera, eXpresser indica que el modelo ha sido generalizado.

■ Actividades para el grupo de secundaria

Para el grupo de primaria se ofrecieron actividades con materiales tales como numeración maya, fracciones y eXpreser (véase la Figura 2). Para el grupo de secundaria, las actividades incluyeron el problema del agente viajero mediante la app de Google Maps y la hoja de cálculo Excel (véanse las figuras 3 y 4).

Figura 2. La apariencia en eXpresser de "Modelo general" (izquierda) y "Mi modelo" (derecha)

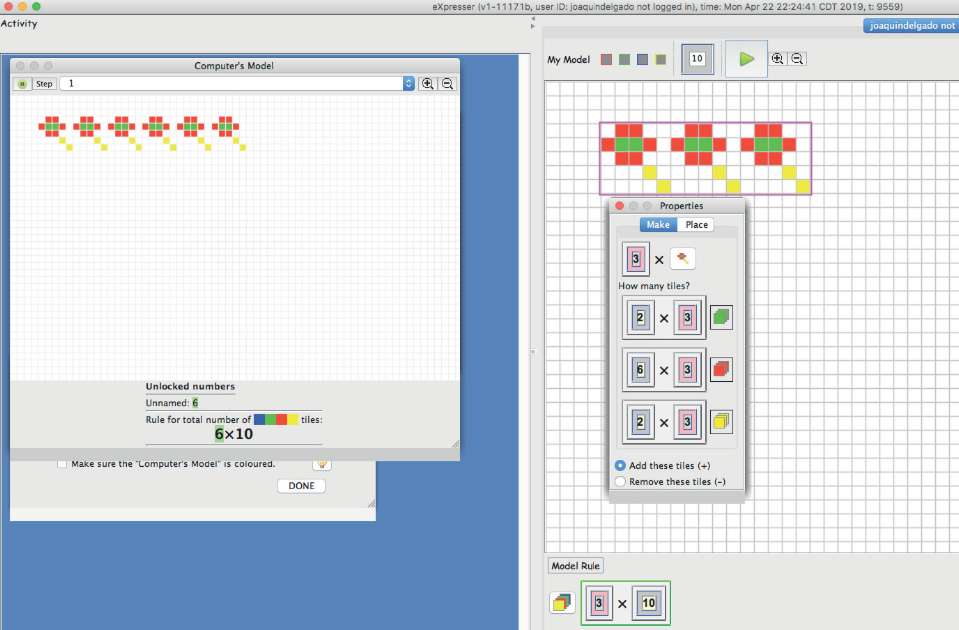
Fuente: Elaboración propia

Fuente: Elaboración propia

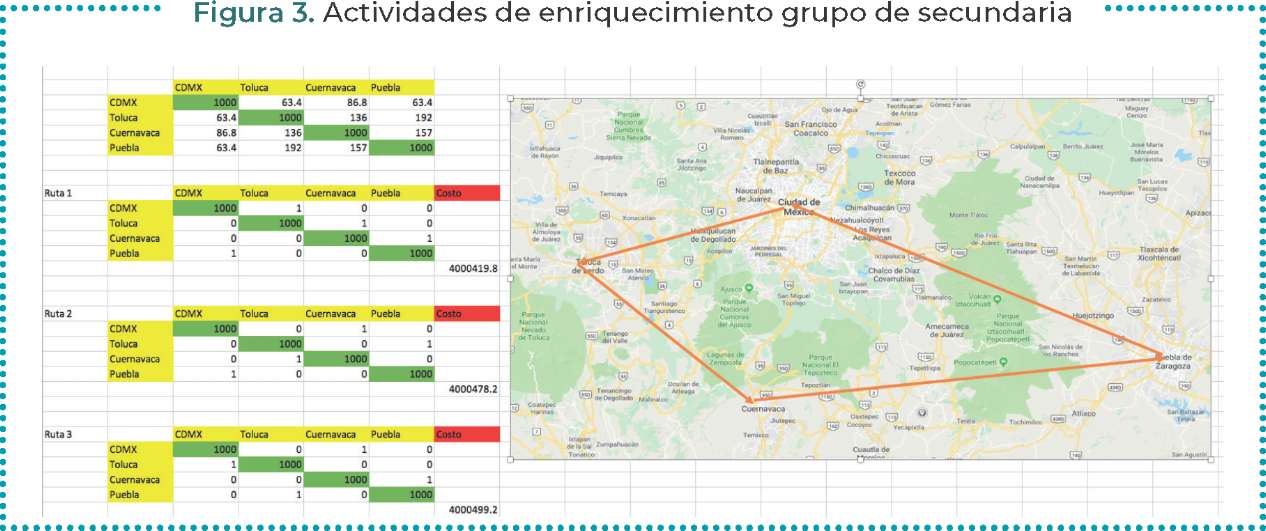
Figura 4. Ejemplo de la actividad del agente viajero grupo de secundaria

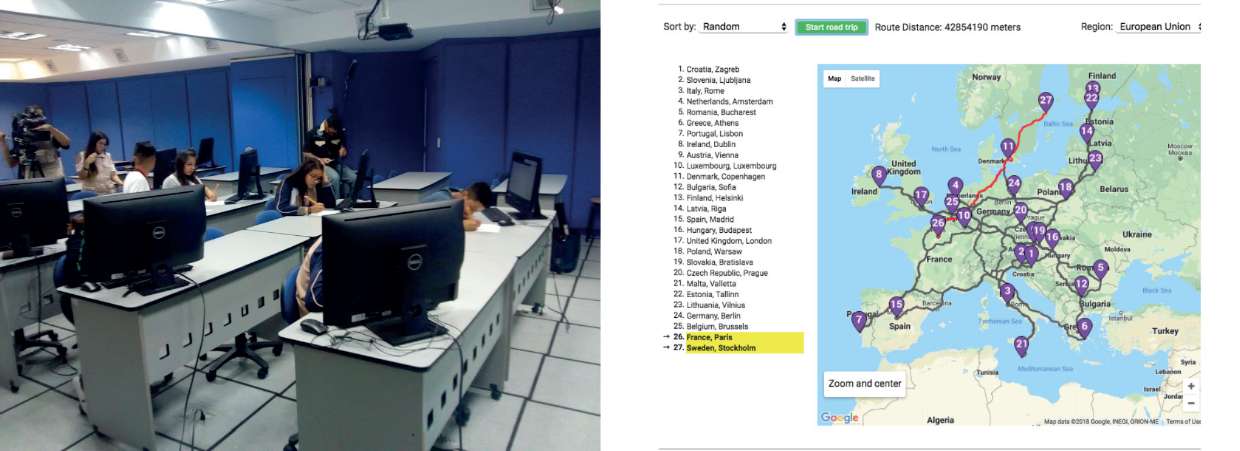
Ejemplo de la actividad problema del agente viajero. Grupo de Secundaria

CS: Traveling; computational thinking for Educators.

Fuente: Elaboración propia

■ Actividades para el grupo de secundaria

En el grupo de alumnos de secundaria se trabajó con una versión simplificada del "problema del agente viajero", con la idea de que los alumnos reconocieran: (a) la complejidad del número de trayectorias posibles, (b) el cálculo de las distancias de recorrido para cada trayectoria para determinar la trayectoria de recorrido mínimo y (c) la desigualdad del paralelogramo para determinar que una ruta es más corta que otra. Primeramente, los alumnos usaron la app de Computational Thinking for Educators CS: Traveling¹. En esta aplicación los alumnos seleccionan una región del mundo, por ejemplo Europa, y ordenan las ciudades por longitud, por latitud o al azar. Los alumnos pueden arrastrar con el ratón el orden en el que las ciudades serán recorridas por el agente viajero. Una vez ordenadas la aplicación tiene un botón que ejecuta un programa que hace uso de Google Maps para contar el número de kilómetros recorridos en la trayectoria seleccionada. De esta manera los alumnos puedes evaluar el costo en kilómetros para determinar cuál es la mejor estrategia.

En una segunda sesión, los alumnos trabajan de manera más "manual". Se les pide que seleccionen con Google Maps, una región central del país (México) que contenga cuatro ciudades principales (Ciudad de México, Cuernavaca, Puebla y Toluca, en concreto). Con ayuda del ratón, los alumnos pueden medir las distancias entre ciudades en línea recta y con ello construyen con la hoja de cálculo Excel una matriz de 4 x 4 que contiene las distancias de una ciudad a otra. Se motiva a los alumnos para que interpreten la simetría de la matriz como la propiedad de simetría de la distancia entre ciudades. Para fines de cálculo se asignan números grandes a la diagonales esta será la matriz de distancias recorridas (primera matriz de la Figura 3). En seguida, por cada ruta se copia la matriz de costos y se rellena de ceros los elementos fuera de la diagonal y se pone un 1 para indicar el origen y destino consecutivos para construir la ruta (por ejemplo, para la Ruta 1 de la Figura 3, leemos la ruta CDMX -Toluca- Cuernavaca - Puebla- CDMX). Finalmente se multiplican la matriz de distancias y la matriz de Ruta elemento a elemento y se suman (no confundir con la multiplicación matricial), para ello se hace uso de la función SUMAPRODUCTO de Excel. De esta manera se pueden calcular las distancias para las distintas rutas que los alumnos puedan construir. Como Ejercicio final, el instructor motiva dos preguntas. (a) ¿Cuál es el número de rutas posibles?, se puede dar una regla para el número de rutas posibles para 5 ciudades, para 6 ciudades,...? (b) Para las cuatro ciudades cuál ruta es más larga: en la que se visitan las ciudades en diagonal o por los lados?

Análisis y procesamiento de la información de la primera etapa del estudio

Para el análisis de los datos se utilizó el paquete estadístico SPSS, versión 20. Se usaron estadísticas descriptivas a fin de describir el comportamiento de las variables analizadas en la muestra y en los subgrupos. Además, se analizaron las diferencias por sexo en las áreas de percepción de apoyo familiar. Estas se realizaron por medio de pruebas de comparación de medias para muestras independientes. Se aplicó un análisis de varianza simple con el propósito de verificar las diferencias entre los alumnos en las ocho categorías. Posteriormente, se aplicaron pruebas de comparaciones múltiples de Bonferroni para identificar dónde se ubicaban las diferencias. Finalmente, se calcularon las correlaciones, con el objetivo de verificar las asociaciones entre las diferentes variables tanto en la muestra general como en los distintos contextos educativos. Se realizaron los siguientes tipos de análisis:

■ Análisis de cuestionario de estilos de aprendizaje (EA). Se analizó la consistencia interna del instrumento con la finalidad de corroborar la validez de los datos presentados; la escala obtuvo un alfa de Cronbach de 0,870, e indica una validez interna.

■ Análisis de nominación por parte de profesores y compañeros. Se comparó la nominación de profesores y de compañeros.

■ Calificaciones en matemáticas. Se analizaron las calificaciones de los estudiantes como un factor que permite determinar el talento matemático. Se obtuvo el promedio de las calificaciones por escuela y el grado escolar. En la escuela de la Ciudad de México, los estudiantes de cuarto, quinto y sexto grado obtuvieron un promedio de nueve. En la escuela del Estado de México, los estudiantes de primer y segundo grado de secundaria obtuvieron un promedio de nueve.

■ Análisis de escala de percepción de apoyo familiar (PAF). Para la escala de apoyo familiar se realizó un análisis de consistencia interna del instrumento a fin de corroborar la validez de los datos. La escala de apoyo familiar (PAF) obtuvo un alfa de Cronbach de 0,860, lo cual indica una considerable validez interna. También se analizó la correlación general entre los cuatro constructos en contraste con los cuatro constructos del instrumento de PA, que son: activo, reflexivo, teórico y práctico.

Análisis y procesamiento de la información de la segunda etapa del estudio

El análisis de la segunda etapa del estudio se realizó por medio de las hojas de trabajo. Los estudiantes trabajaron en parejas y resolvían las actividades propuestas en los talleres de matemáticas. El análisis de los datos consistió en analizar las respuestas de los estudiantes, así como la interacción social entre ellos.

Resultados de la Primera etapa: identificación del talento matemático

Resultados del cuestionario de apoyo familiar y cuestionario de estilos de aprendizaje

El cuestionario de apoyo familiar (PAF) alcanzó un alfa de Cronbach de 0,860, lo que indica una considerable validez interna, mientras que la escala de estilos de aprendizaje obtuvo un alfa de Cronbach de 0,870; esto refiere que ambos instrumentos tienen una adecuada validez interna.

Con respecto a los estilos de aprendizaje que clasificaron en "reflexivo" y "teórico", según Alonso et al. (2007) el estudiante con estilo de aprendizaje reflexivo pone mucha atención y cuidado en las tareas que realiza, es analítico, observador, detallista y propenso a investigar; mientras que el estudiante con un estilo de aprendizaje teórico es metódico, lógico, objetivo, crítico, estructurado, sistemático, cuestiona los procedimientos que aprende y propone nuevos.

Para el total de la muestra se encontró que hubo una correlación de Pearson alta entre el estilo de aprendizaje reflexivo con los constructos de apoyo familiar "proporcionar tiempo" y "espacio para el estudio", con 0,323. También hubo una correlación significativa entre el estilo reflexivo y el constructo de apoyo familiar "evaluación y repaso", en el que se obtuvo una correlación de Pearson de 0,224. Por su parte, el estilo de aprendizaje teórico tuvo una alta correlación con tres de los cuatro constructos evaluados por la escala de apoyo familiar; estas correlaciones son con "asistencia o apoyo en tareas escolares", "tiempo y espacio para el estudio" y "evaluación y repaso". En el caso específico de los alumnos de quinto grado, la mayor correlación fue entre el estilo de aprendizaje reflexivo con el constructo de "tiempo y espacio para el estudio", al presentar una correlación de Pearson de 0,260 con una significancia bilateral de 0,023.

Resultados del cuestionario de generalización

A partir de las respuestas de los estudiantes, obtenidas en la entrevista clínica individual, se cate-gorizaron las respuestas y se obtuvieron dos tipos de estrategias:

■ Estrategia aditiva. En este tipo de respuesta los estudiantes resuelven los problemas planteados mediante sumas y restas explícitas o mentales, o con conteo. Se manifiesta un pensamiento aditivo o aritmético.

■ Estrategia prealgebraica. En esta categoría los estudiantes resuelven los problemas con una multiplicación y establecen relaciones proporcionales, comprenden la idea de variable como número general y como una relación funcional, pero se les dificulta encontrar una regla general y expresarla de forma verbal o escrita.

Resultados de la validación del instrumento de procesos de generalización

Se realizó un análisis de consistencia interna del instrumento de procesos de generalización. Este mostró un muy buen indicador de consistencia interna para dos dominios (relación cuadrática y variable o número general, ambos con un coeficiente alfa de Cronbach de 0,80 y 0,73, respectivamente), y con indicadores aceptables para dos dominios (sucesión aritmética creciente y decreciente de 0,64, y para figuras de sucesión de 0,58). Posee un coeficiente alfa de Cronbach de 0,83 en todo el instrumento, lo cual significa que hay buena consistencia interna del instrumento para medir indicadores de procesos de generalización en estas tareas y en las cuatro diferentes dimensiones: "sucesión aritmética creciente y decreciente", "sucesión aritmética", "relación cuadrática" y "variación de número general".

Resultados del cuestionario sobre procesos de generalización: estrategias de resolución de problemas

A continuación, se presentan los resultados obtenidos en el cuestionario de procesos de generalización.

............... Figura 5. Respuestas de los alumnos al ...............

■ cuestionario sobre procesos de generalización j

Estrategias de resolución de problemas

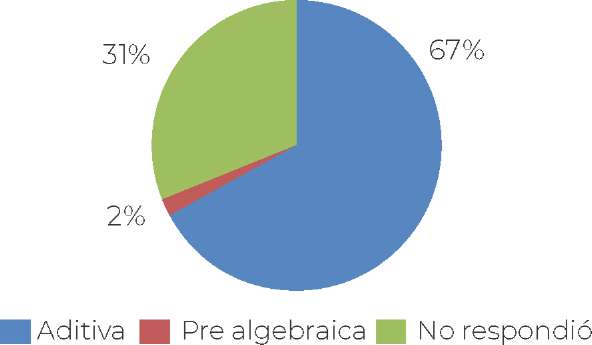
Fuente: Elaboración propia

Los resultados obtenidos se muestran en la Figura 5. La mayoría de los estudiantes, el 67% de la muestra, proporciona una respuesta de tipo aditivo; un 31% no responde a las preguntas o no termina de resolver el problema en razón a su complejidad; y solo un 2% de los alumnos proporciona una respuesta de tipo pre-algebraico. Este es el porcentaje que tamizamos como alumnos con talento matemático, porque están en la transición del pensamiento multiplicativo al pre-algebraico, de acuerdo con su edad (Butto y Delgado, 2012).

Ejemplo de identificación de una secuencia. Pregunta 1

Contenido matemático: se pide completar sucesiones aritméticas crecientes y decrecientes. En la Figura 6 se muestran las respuestas de Liza y Luis.

Figura 6. Problema 1. Identificación de sucesiones de Liza (izquierda) y Luis (derecha) 1) Completa las siguientes secuencias. 1) Completa las siguientes secuencias.

Comentario: Luis identifica la sucesión decreciente que incluye términos negativos (c), a diferencia de Liza. En la sucesión decreciente de términos positivos (d), Luis yerra en el cálculo del último término.

Ejemplo de pensamiento aditivo y multiplicativo. Pregunta 2

Contenido matemático: comparación del crecimiento una sucesión aritmética y una sucesión geométrica.

Se pide al estudiante observar cuatro figuras de sucesiones aritméticas y geométricas de puntos y se le solicita continuarlas. En la Figura 7 se muestra una respuesta de Liza y Luis.

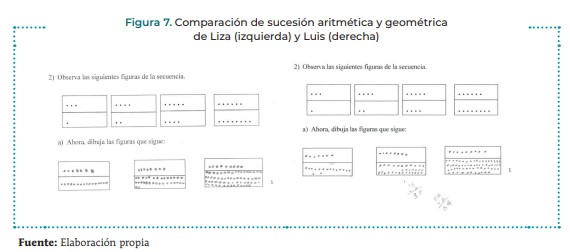
Liza realiza el cálculo mental del quinto término de la serie geométrica (16 = 2 x 8) y hace explícito el cálculo recursivo de los siguientes términos (32 = 2 x 16; 64 = 2 x 32), por tanto, muestra un pensamiento multiplicativo. Luis no explicita los cálculos y dibuja sesenta y tres puntos en vez de sesenta y cuatro, lo que evidencia su pensamiento aditivo.

Ejemplo de estrategia prealgebraica. Pregunta 3

Contenido matemático: sucesiones aritmética y geométrica en variación conjunta.

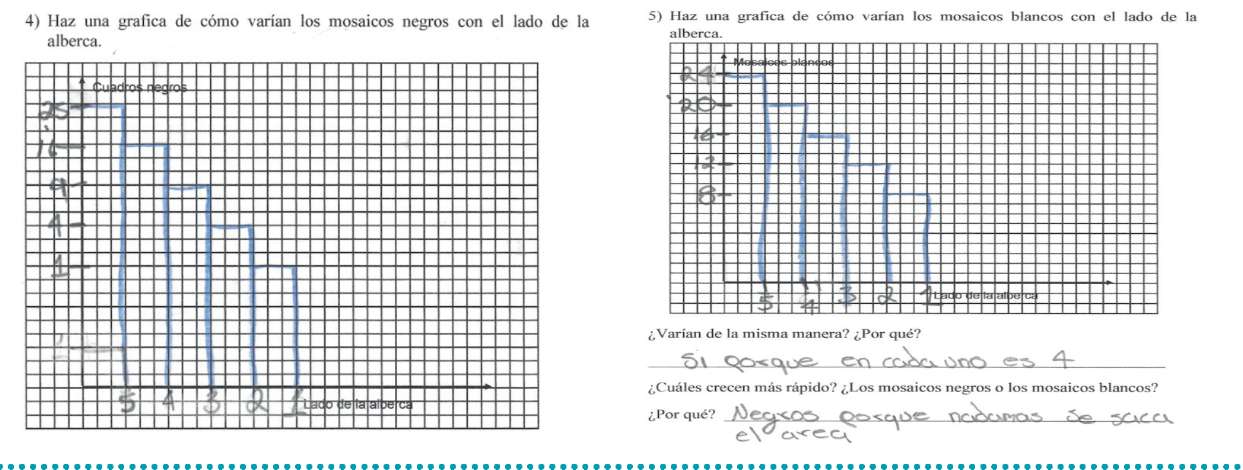
Se le pide al estudiante observar tres albercas de distintos tamaños y, a partir de estas, dibujar las albercas 4 y 5; posteriormente, se le pide graficar la variación de cuadros negros con blancos, que llene una tabla de valores y responda una serie de preguntas. En la Figura 8 se muestran los resultados de Liza, quién alcanzó esta categorización.

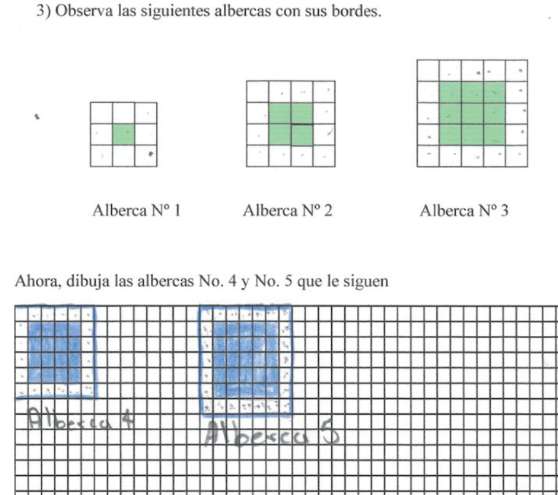
Figura 8. Respuestas de Liza al problema de las albercas

Fuente: Elaboración propia

Liza completa la sucesión de albercas y consigue representar la variación de cuadros blancos y negros (azul en el dibujo) con la alberca, lo cual muestra su dominio en dos niveles de representación de la variación: pictórico y gráfico. Además, puede separar claramente la variación del número de cuadros blancos y azules de la variación conjunta, representada en la sucesión pictórica. En la Figura 9 se muestra la tabla de respuestas de Liza. Sus respuestas hacen uso de tres variables en la relación C = N + B, donde N es el número de cuadros negros, B el número de cuadros blancos y C el número total de cuadros negros y blancos (las columnas en ese orden). Liza hace uso de las relaciones N = C - N, B = C - N en sus respuestas a los incisos (a) y (b). En los incisos (c) y (d) no alcanza a dar totalmente la regla, pero usa el hecho de poder calcular el total de cuadros usando la fórmula lado x lado.

............... Figura 9. Tabla de respuestas de Liza ...............

• al problema de las albercas j

3} Llena la tabla con los siguientes datos.

a) ¿Cómo vas obteniendo el número de mosaicos blancos?

(–■) Tn_CCNOa ç\ èi€ fio* ci\c e>e> neg^ci^ ^'

b) ¿Cómo vas obteniendo el número de mosaicos negros?

c) ¿Cómo encuentras el número de mosaicos blancos si conoces el lado de la alberca?

d) ¿Cómo encuentras el número de mosaicos negros si conoces el lado de la alberca?

Fuente: Elaboración propia

Segmento de la entrevista de Liza (diez años)

E: ¿Qué hiciste para poder dibujar las albercas 4 y 5?

N: Vi las primeras tres y me fijé como iba creciendo.

E: ¿Cómo iban creciendo?

N: [Señala la alberca] Los bordes iban aumentando más cuatro en todas, y el centro de la dos se multiplica, el centro de la uno por cuatro y luego la tres, la cuatro y la cinco al doble más uno.

E: Si yo te pidiera dibujar la alberca seis, ¿cómo lo harías? N: Igual.

E: ¿Cómo es igual? ¿Qué tendrías que hacer para saber cuál es el número de cuadrados blancos y verdes de la alberca seis?

N: Para los blancos de la seis sumar el número de cuadrados de la cinco más cuatro, y para el centro el doble de la cinco más uno.

E: ¿Cómo hiciste las gráficas? ¿Qué datos tomaste o que hiciste para hacer la primera gráfica y la segunda?

N: Para la primera me fijé en las albercas y conté los cuadrados negros, y para la segunda hice lo mismo, pero aquí me fijé en los cuadros blancos.

E: ¿Varían de la misma manera los cuadros negros y los cuadros blancos?

N: Sí, porque en cada uno es cuatro.

E: ¿Cuáles crecen más rápido? ¿Los cuadros negros o los cuadros blancos? N: Negros, porque nada más se saca el área de la alberca. E: ¿Cómo llenaste la tabla? ¿Qué datos utilizaste para llenarla?

N: Me fije en las albercas, primero ponía cuantos cuadros blancos y negros, y luego solo los negros y luego solo los blancos.

E: ¿Como vas obteniendo el número de cuadros negros?

N: Restando el número de mosaicos negros y blancos menos el número de mosaicos blancos.

E: ¿Cómo encuentras el número de mosaicos blancos si conoces el lado de la alberca?

N: Buscando el área, por ejemplo, si es tres multiplico 3 x 3 = 9 - 1 = 8, y serían ocho mosaicos blancos.

Resultados de la secunda etapa del estudio: eXpresser

La primera sesión, que no se reporta aquí, incluyó actividades de familiarización con el ambiente eXpresser. A continuación, se muestran algunas hojas de trabajo y se describen las respuestas de los estudiantes a las actividades propuestas en los talleres de matemáticas.

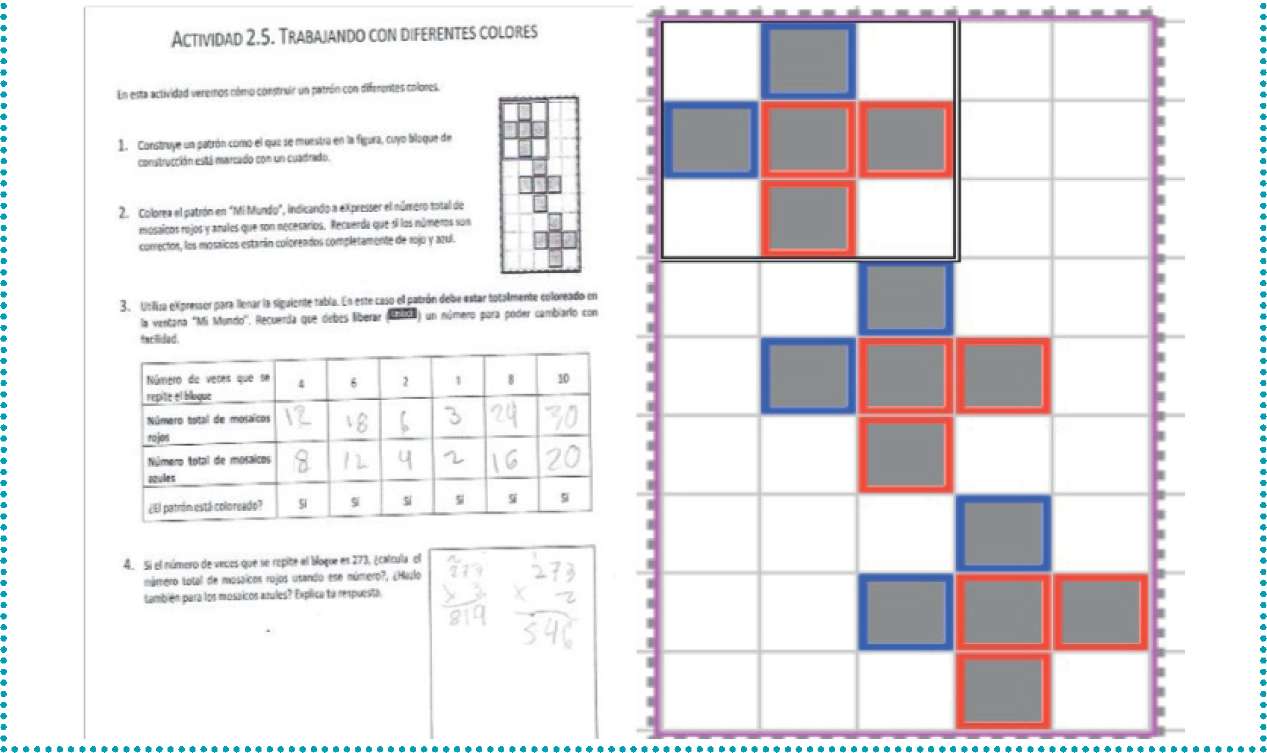
Figura 10. Hoja de trabajo de actividad en eXpresser. a) repetir un bloque cuadrado; b) hoja de respuestas

Fuente: Elaboración propia

En la actividad mostrada en la Figura 10 se pide al alumno construir un bloque en forma de un cuadrado de 3 x 3 que contiene celdas rojas y azules, y después repetirlo para formar un patrón (véase la Figura 10a). El alumno debe decidir cuántas celdas a la derecha y a la izquierda mover el bloque para que no se traslapen, así como predecir el número de celdas rojas y azules dependiendo del número de veces que se repite el patrón (x). Se trata de una sucesión aritmética simple, dada por las fórmulas a = 2x, r = 3x, donde x es el número de veces que se repite el bloque, a es el número de bloques azules y r es el número de bloques rojos. En las hojas de respuestas de la Figura 10b, pregunta 3, se le pide al estudiante rellenar la tabla conteniendo las filas x, a, r de las sucesiones. Cuando x es pequeño el alumno puede experimentar con eXpresser para verificar su respuesta, pero para valores grandes como x = 30, que se muestran en la tabla de la Figura 10b, el alumno se ve forzado a proponer una regla. Específicamente, para x = 273, en la pregunta 4, Figura 9b, se muestra el cálculo hecho por el alumno para obtener los valores de a y r.

En la Figura 11 se muestra una actividad similar, pero al alumno se le da libertad de construir el bloque inicial. En la Figura 10a el alumno construye un bloque cuadrado de 3 x 3, pero usa siete colores amarillos y dos verdes.

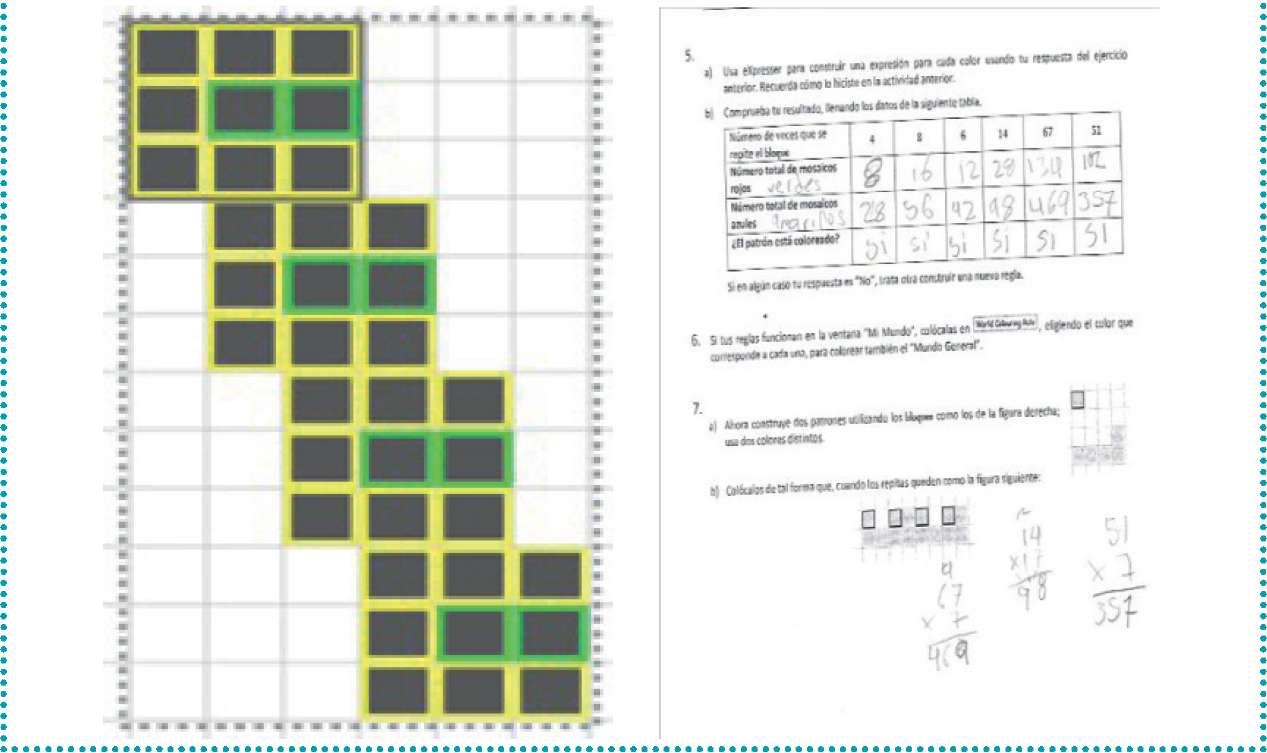
Figura 11. Hojas de trabajo de actividad en eXpresser. a) repetir un bloque diseñado por el estudiante; b) hoja de respuestas

Fuente: Elaboración propia

Las reglas de las sucesiones aritméticas son a = 7x, v = 2x, donde x es el número de veces que se repite el bloque, a es el número de celdas amarillas, v el número de celdas verdes. En la hoja de respuestas (Figura 10b, pregunta 5), el alumno llena la tabla conteniendo las filas de estas sucesiones. Los cálculos del alumno para la sucesión a = 7x, para los valores de x = 67, 14, 51, se muestra en la parte inferior de la hoja de trabajo en la Figura 10b, lo cual muestra que el alumno es capaz de usar la regla.

Resultados de la secunda etapa del estudio: problema del acente viajero usando la app de Goocle Maps y la hoja de cálculo Excel

En una primera sesión, los alumnos usaron la suite de Google Computational Thinking for Educators y seleccionaron "Europa". El programa contiene una lista de ciudades y los alumnos escogen un ordenamiento de la lista por longitud, latitud y de forma aleatoria. Luego ellos ordenan, arrastrando el ratón, los ítems de la lista para definir el orden de recorrido. Al finalizar la ordenación, el programa calcula las distancias de la ruta y arroja el resultado en kilómetros. Así, los alumnos pueden experimentar con la dificultad del problema. Casi siempre la elección inicial aleatoria arroja el peor resultado. Los alumnos comprenden la necesidad de una estrategia. Aunque ellos no llegan a explicitarla, la mayoría usa una estrategia de minimización local.

En otra variante del problema y en una segunda sesión, los alumnos seleccionaron un mapa de México de Google Maps y unas pocas ciudades (Ciudad de México, Toluca, Cuernavaca, Puebla), a fin de trazar las posibles rutas con origen y destino a la Ciudad de México (CDMX).

Conclusiones

En lo que se refiere a la primera etapa del estudio, los resultados revelan que los estudiantes con talento matemático tienen habilidades matemáticas por encima de su nivel de conocimiento, específicamente en lo que se relaciona con los procesos de generalización. Los estudiantes con talento poseen un nivel conceptual alto de las ideas exploradas en el instrumento, así como de las estrategias de resolución de los problemas, en los cuales las estrategias pre-algebraicas en ese nivel escolar explorado (quinto grado de primaria) revelaron que los estudiantes comprenden ciertas ideas algebraicas. Además, utilizaron estrategias de resolución de problemas creativas e intentaron resolver los problemas planteados de manera autónoma, mientras que los demás alumnos recurren a estrategias, principalmente aditivas, y recurren a procedimientos de acierto y error sin ninguna o poca reflexión conceptual de sus procedimientos.

En lo referente a los estilos de aprendizaje, los estudiantes con talento matemático poseen un estilo de aprendizaje reflexivo y teórico; es decir, tienen un interés y dominio por un tema en específico, procesos de resolución ingeniosos e interés por aprender. Es importante destacar que estos estudiantes cuentan con apoyo familiar de sus padres en las tareas escolares, y esto favorece el desarrollo de sus habilidades.

En lo que refiere a la segunda etapa del estudio, a partir de los resultados reportados podemos hacer algunas recomendaciones para el salón de clases de matemáticas con la finalidad de que los alumnos puedan desarrollar el pensamiento computacional, y que este desarrollo pueda potenciar no solo el desarrollo del pensamiento matemático, sino de muchos otros contenidos que están en los planes y los programas de estudios vigentes de la Secretaría de Educación Pública de México.

Una de estas consideraciones es que los estudiantes puedan acercarse a la resolución de problemas matemáticos en entornos tecnológicos de aprendizaje como, por ejemplo, el de la plataforma Google, y resolver actividades como el problema del agente viajero.

Otra consideración es permitir el trabajo colaborativo entre alumnos en las clases de matemáticas como una manera de presentar las diversas resoluciones a un mismo problema, a fin de llegar a una formalización matemática. Además, se sugiere poner énfasis tanto en los procedimientos de resolución como considerar el papel que juega el error, en cuanto es una fuente de aprendizaje y, así, a partir del error, permitirle a los alumnos reflexionar sobre sus propios procesos de resolución.

¹ https://computationalthinkingcourse.withgoogle.com/unit?unit=2&lesson=3

Referencias

Alonso, C., Gallego, D. & Honey, P. (2007). Los estilos de aprendizaje. Procedimientos de diagnóstico y mejora (7^a ed.). Bilbao: Ediciones Mensajero. Recuperado de: https://www.researchgate.net/publication/311452891

Bazán, A., Sánchez, B. & Castañeda, S. (2007). Relación estructural entre apoyo familiar, nivel educativo de los padres, características del maestro y desempeño en lengua escrita. Revista Mexicana de Investigación Educativa, 33(12), 701-729.

Bednarz, N., Kieran, C. & Lee, L. (1996). Approaches to algebra. Perspectives for Seeing. Harmondsworth, Middlesex: BBC y Penguin Books.

Benavides, M., Ríos, C. & Marshall, M. (2004). La educación de niños con talento en Chile. En M. Benavides, A. Maz, E. Castro, y R. Blanco (eds.), La educación de los niños con talento en Iberoamérica (pp. 105-114). Santiago, Chile: Editorial Trineo S.A.

Butto, C. & Delgado, J. (2012). Rutas hacia el álgebra. Actividades en Excel y Logo. México: UPN-Conacyt.

Butto, C., Delgado, J. & Bazán, A. (2018). Procesos de generalización: una vía de acceso al pensamiento algebraico temprano en educación básica. Horizontes Pedagógicos, 20(1), 25-36.

Castro, E., Rico, L. & Castro, E. (1995). Estructuras aritméticas elementales y su modelización. Bogotá: Editorial Iberoamericana.

Delval, J. (2001). La realización de la entrevista. Descubrir el pensamiento de los niños (pp. 113-139). España.: Ed. Paidós.

De la Torre, G., Del Valle, L., Carpinteyro, S. & Mijangos, A. (2017). Programa adopte un talento: un vínculo entre la comunidad científica y los niños. Revista Digital Universitaria, 18(7). Recuperado de: http://revista.unam.mx/vol.18/num7/art56/index.html

Fernández, M. & Pérez, A. (2011). Las altas capacidades y el desarrollo del talento matemático. El Proyecto Estalmat-Andalucía. Revista Iberoamericana de Educación matemática. 27.

Geraniou, E., Mavrikis, M., Noss, R. & Hoyles, C. (2009). A learning environment to support mathematical generalization in the classroom. En Proceedings of CERME 6. Lyon, France. Recuperado de: http://ife.ens-lyon.fr/publications/edition-electronique/cerme6/wg7-09-geranioumavrikis-hoylesnoss.pdf

Grigorenko, E. L. (2017). Gifted education in Russia: developing, threshold, or developed. Cogent Education, 4(1), 1364898.

Hernández, R., Fernández, C. & Batista, P. (2014). Metodología de la investigación. México: McGraw Hill.

MacGregor, M. & K. Stacey. (1993). Seeing to pattern and writing to rule. Proceeding of Psychology of Mathematics Education. Ibaraki, Japón.

Mason, J., Graham, A., Pimm, D. & Gower, N. (1985). Routes to roots of algebra. U.K: The Open University Press.

Marland, S. P. Jr. (1971). Education of the gifted and talented-Vol 1 (Report to the Congress of the United States by the U.S. Commissioner of Education).

National Association for Gifted Children (NAGC). A brief history of gifted and talented education. Recuperado de: http://www.nagc.org/resources-publications/resources/gifted-education-us/brief-history-gifted-and-talented-education

National Council of Teachers of Mathematics. (1989). National standards for mathematics. National Council of Teachers of Mathematics.

Noss, R., Poulovassilis, A., Geraniou, E., Gutierrez-Santos, S., Hoyles, C., Kahn, K. y Mavrikis, M. (2011). The design of a system to support exploratory learning of algebraic generalization. Computers & Education, 59(1), 63-81.

Núñez, R., Pérez, J., Luque, C., & Arévalo, J. (2004). El Semicírculo de la Universidad Sergio Arboleda. Revista Electrónica de Difusión Científica. Recuperado de: https://repository.usergioarboleda.edu.co/bitstream/handle/11232/300/CienciasSociales%20y%20Humanas244.pdf?sequence=1&isAllowed=y

Núñez, R., Gómez-Bermeo, L. V. & Cortés, C. M. (2011). El ambiente académico universitario clave del talento matemático. En Memorias XIII CIAEM. Recife, PE, Brasil. Recuperado de: https://ciaem-redumate.org/ocs/index.php/xiii_ciaem/xiii_ciaem/paper/viewFile/2499/605

Regianni, M. (1994). Generalization as a basic for algebraic thinking: observations with 11-12 years old pupils. En Conference Proceeding of the XVIIIPME (pp. 97-104). Lisboa, Portugal.

Renzulli, J. (2008). La educación del sobredotado y el desarrollo del talento para todos. Revista de Psicología, 26(1), 23-44.

Renzulli, J. S. & Reis, S. M. (1985). The schoolwide enrichment model: A comprehensive plan for educational excellence. Mansfield Center, CT: Creative Learning Press.

Secretaría de Educación Pública (2011). Estrategia de atención para alumnos y alumnas con capacidades y aptitudes sobresalientes en la educación básica del D. F. México, D. F.: Secretaría de Educación Pública.

Ushakov, D. V. (2010). Olympics of the mind as a method to identify giftedness: Soviet and Russian experience. Learning and Individual Differences, 20, 337-344